题目内容
13.下列四组函数,表示同一函数的是( )| A. | $f(x)=\sqrt{x^2},g(x)=x$ | B. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x+1$ | ||
| C. | $f(x)=\sqrt{{x^2}-4},g(x)=\sqrt{x+2}\sqrt{x-2}$ | D. | $f(x)=lg2-lgx,g(x)=lg\frac{2}{x}$ |
分析 根据两个函数的定义域相同、对应关系也相同,即可判断它们是同一个函数.
解答 解:A组中两函数的定义域相同,对应关系不同,f(x)=|x|,故不是同一函数;
B组中f(x)的定义域为{x|x≠1},g(x)的定义域是R,定义域不同,不是同一函数;
C组中f(x)的定义域是{x|x≤-2或x≥2},g(x)的定义域是{x|x≥2},两函数的定义域不同,不是同一函数;
D组中f(x)=lg2-lgx=lg$\frac{2}{x}$(x>0),g(x)=lg$\frac{2}{x}$(x>0),两函数的定义域相同,对应关系也相同,是同一函数.
故选:D.
点评 本题考查判断两个函数是否为同一函数的问题,是基础题目.

练习册系列答案
相关题目
1.某几何体的三视图如图所示,该几何体的体积为( )


| A. | 24 | B. | $\frac{70}{3}$ | C. | 20 | D. | $\frac{68}{3}$ |
18.若数列{an}满足an+2=2•$\frac{{{a_{n+1}}}}{a_n}$(n∈N*),且a1=1,a2=2,则数列{an}的前2016项之积为( )
| A. | 22014 | B. | 22015 | C. | 22016 | D. | 22017 |
2.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{y≥a(x-4)}\end{array}\right.$,若z=2x+y的最小值是-1,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
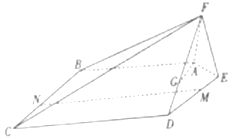 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.