题目内容
X大学2014年自主招生报名刚结束，某考生想知道这次报考的人数，他随机记录了50个考生的考号；已知考生的考号是从0001，0002，0003，…这样从小到大依次顺序排列．经计算，这50个考号的和是24966（其中0001+0002视为3），据此，估计2014年参加X大学自主招生的考生数约为（ ）
| A、500人 | B、1000人 |
| C、1500人 | D、2000人 |
考点：离散型随机变量的期望与方差
专题：概率与统计
分析：由题意知先求平均数，再估计中位数，再求出考生的大约人数．
解答：
解：由题意知，
考生的考号是从0001，0002…从小到大排列的，50个考生的考号和为24966，
≈500，
此平均数是考生的平均数，应是中位数，故大约有2×500=1 000人．
故选：B．
考生的考号是从0001，0002…从小到大排列的，50个考生的考号和为24966，
| 24966 |
| 50 |
此平均数是考生的平均数，应是中位数，故大约有2×500=1 000人．
故选：B．
点评：本题考查了平均数和中位数的定义及关系，并用它们来估计总体的容量，是基础题．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
目标函数z=2x+y，变量x，y满足
，则有（ ）
|
| A、zmin=4，无最大值 | ||
B、zmax=
| ||
| C、z既无最大值，也无最小值 | ||
D、zmin=0，zmax=
|
经过点（0，1）且与直线2x-y+3=0垂直的直线方程式（ ）
| A、2x+y-4=0 |
| B、x+2y-2=0 |
| C、x-2y+2=0 |
| D、x-2y-2=0 |
有4条线段长度分别为3，5，7，9，从这4条线段中任取3条，则所取3条线段不能构成一个三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设等差数列{an}的前n项和为Sn，若a5=2，则2S6+S12=（ ）
| A、6 | B、12 | C、24 | D、48 |
已知等比数列{an}满足a2•a6=ak2，则整数k的值是（ ）
| A、2 | B、3 | C、4 | D、5 |
设等差数列{an}的前n项和为Sn，且a1=2，若数列{Sn}也为等差数列，则S2014=（ ）
| A、1007 | B、2014 |
| C、4028 | D、0 |
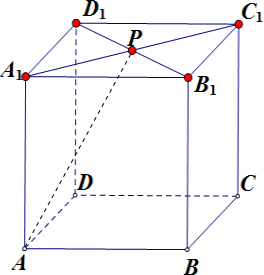在一个正方体ABCD-A1B1C1D1中，P为正方形A1B1C1D1的中心，求证AP⊥PB1．