题目内容
己知F1,F2为椭圆C:
+
=1(a>b>0)的左、右焦点,点A为椭圆C上的动点,且当点A在y轴上时,
•
=2S △F1F2A
(1)求椭圆C的离心率;
(2)己知
•
的最大值为1,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| F1A |
| F1F2 |
(1)求椭圆C的离心率;
(2)己知
| AF1 |
| AF2 |
考点:椭圆的简单性质,向量在几何中的应用
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意可取A(0,b),F1(-c,0),F2(c,0).由于S△F1F2A=
×2c×b=bc.
•
=2S △F1F2A,利用数量积运算可得2c2=2bc,解得a,b,c即可..
(2)利用数量积的性质可得:
•
≤|
| |
|,取等号时,点A为椭圆位于椭圆的右端点,而|
| |
|=(a-c)(a+c)=1,可得
,解得即可.
| 1 |
| 2 |
| F1A |
| F1F2 |
(2)利用数量积的性质可得:
| AF1 |
| AF2 |
| AF1 |
| AF2 |
| AF1 |
| AF2 |
|
解答:
解:(1)由题意可取A(0,b),F1(-c,0),F2(c,0).
∴
=(c,b),
=(2c,0),S△F1F2A=
×2c×b=bc.
∵
•
=2S △F1F2A,
∴2c2=2bc,解得b=c
.∴a=
=
c.
∴e=
=
.
(2)
•
=|
| |
|cos∠F1AF2≤|
| |
|,取等号时,点A为椭圆位于椭圆的右端点,
∴|
| |
|=(a-c)(a+c)=1,
联立
,
解得b=c=1,a2=2.
∴椭圆C的方程为
+y2=1.
∴
| F1A |
| F1F2 |
| 1 |
| 2 |
∵
| F1A |
| F1F2 |
∴2c2=2bc,解得b=c
.∴a=
| b2+c2 |
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
(2)
| AF1 |
| AF2 |
| AF1 |
| AF2 |
| AF1 |
| AF2 |
∴|
| AF1 |
| AF2 |
联立
|
解得b=c=1,a2=2.
∴椭圆C的方程为
| x2 |
| 2 |
点评:本题考查了椭圆的标准方程及其性质、向量的数量积运算及其性质、三角形的面积计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
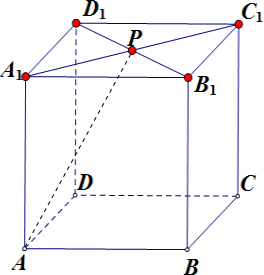 在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.
在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1. 双曲线
双曲线