题目内容
利用三角函数线证明:|sinα|+|cosα|≥1.
考点:三角函数线
专题:三角函数的求值
分析:如图所示,当角α的终边在坐标轴上时,|sinα|+|cosα|=1.当角α的终边落在四个象限时,利用三角形两边之和大于第三边有:|sinα|+|cosα|>1,综合可得结论.
解答:
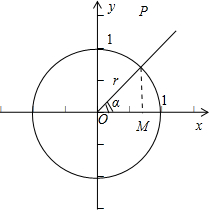 证明:当角α的终边在坐标轴上时,正弦线(余弦线)变成一个点,
证明:当角α的终边在坐标轴上时,正弦线(余弦线)变成一个点,
而余弦线(正弦线)的长等于r(r=1),
所以|sinα|+|cosα|=1.
当角α的终边落在四个象限时,设角α的终边与单位圆交于
点P(x,y)时,过P作PM⊥x轴于点M(如图),
则|sinα|=|MP|,|cosα|=|OM|,利用三角形两边之和大于第三边有:|sinα|+|cosα|=|MP|+|OM|>1,
综上有|sinα|+|cosα|≥1.
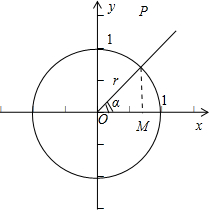 证明:当角α的终边在坐标轴上时,正弦线(余弦线)变成一个点,
证明:当角α的终边在坐标轴上时,正弦线(余弦线)变成一个点,而余弦线(正弦线)的长等于r(r=1),
所以|sinα|+|cosα|=1.
当角α的终边落在四个象限时,设角α的终边与单位圆交于
点P(x,y)时,过P作PM⊥x轴于点M(如图),
则|sinα|=|MP|,|cosα|=|OM|,利用三角形两边之和大于第三边有:|sinα|+|cosα|=|MP|+|OM|>1,
综上有|sinα|+|cosα|≥1.
点评:本题主要考查任意角的三角函数的定义,用单位圆中的三角函数线表示三角函数的值,属于基础题.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,若a5=2,则2S6+S12=( )
| A、6 | B、12 | C、24 | D、48 |
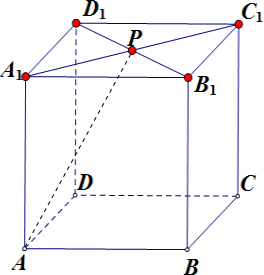 在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.
在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.