题目内容
某小学每天安排5节课,其中上午3节课,下午2节课.现要将音乐课、美术课各1节安排在星期三上.
(1)用树状图或列举法表示出所有可能的排课结果;
(2)求音乐课在上午而美术课恰好在下午的概率.
(1)用树状图或列举法表示出所有可能的排课结果;
(2)求音乐课在上午而美术课恰好在下午的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)有可能的排课结果有20种不同排法,列举法写出所有的排课结果.
(2)由(1)知基本事件总数n=20,音乐课在上午而美术课恰好在下午的不同排法有6种,由此能求出其概率.
(2)由(1)知基本事件总数n=20,音乐课在上午而美术课恰好在下午的不同排法有6种,由此能求出其概率.
解答:
解:所有可能的排课结果有:
第一节音乐.第二节美术;第一节音乐.第三节美术;第一节音乐.第四节美术;
第一节音乐.第五节美术;第二节音乐.第一节美术;第二节音乐.第三节美术;
第二节音乐.第四节美术;第二节音乐.第五节美术;第三节音乐.第一节美术;
第三节音乐.第二节美术;第三节音乐.第四节美术;第三节音乐.第五节美术;
第四节音乐.第一节美术;第四节音乐.第二节美术;第四节音乐.第三节美术;
第四节音乐.第五节美术;第五节音乐.第一节美术;第五节音乐.第二节美术;
第五节音乐.第三节美术;第五节音乐.第四节美术.
共有20种不同排法.
(2)由(1)知基本事件总数n=20,
音乐课在上午而美术课恰好在下午的情况有:
第一节音乐.第四节美术;第一节音乐.第五节美术;第二节音乐.第四节美术;
第二节音乐.第五节美术;第三节音乐.第四节美术;第三节音乐.第五节美术.
共有6种不同排法.
∴音乐课在上午而美术课恰好在下午的概率:
p=
=
.
第一节音乐.第二节美术;第一节音乐.第三节美术;第一节音乐.第四节美术;
第一节音乐.第五节美术;第二节音乐.第一节美术;第二节音乐.第三节美术;
第二节音乐.第四节美术;第二节音乐.第五节美术;第三节音乐.第一节美术;
第三节音乐.第二节美术;第三节音乐.第四节美术;第三节音乐.第五节美术;
第四节音乐.第一节美术;第四节音乐.第二节美术;第四节音乐.第三节美术;
第四节音乐.第五节美术;第五节音乐.第一节美术;第五节音乐.第二节美术;
第五节音乐.第三节美术;第五节音乐.第四节美术.
共有20种不同排法.
(2)由(1)知基本事件总数n=20,
音乐课在上午而美术课恰好在下午的情况有:
第一节音乐.第四节美术;第一节音乐.第五节美术;第二节音乐.第四节美术;
第二节音乐.第五节美术;第三节音乐.第四节美术;第三节音乐.第五节美术.
共有6种不同排法.
∴音乐课在上午而美术课恰好在下午的概率:
p=
| 6 |
| 20 |
| 3 |
| 10 |
点评:本题考查不同的排课结果的求法,考查概率的计算,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
已知等比数列{an}满足a2•a6=ak2,则整数k的值是( )
| A、2 | B、3 | C、4 | D、5 |
下列命题中,正确的是( )
| A、如果两条平行直线中的一条与平面α平行,那么另一条也与平面α平行 |
| B、若两个平面垂直,则一个平面内的任一条直线必垂直于另一个平面 |
| C、若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点 |
| D、垂直于同一平面的两个平面互相平行 |
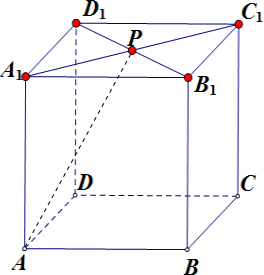 在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.
在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1. 双曲线
双曲线