题目内容
已知椭圆
+
=1(a1>b1>0)与双曲线
+
=1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点
(1)试用b1、b2表示△F1PF2的面积;
(2)当b1+b2=m(m>0)是常数时,求△F1PF2的面积的最大值.
| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
(1)试用b1、b2表示△F1PF2的面积;
(2)当b1+b2=m(m>0)是常数时,求△F1PF2的面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设∠F1PF2=θ,当PF1+PF2=2a1时,S△F1PF2=b12•
,当PF1-PF2=2a2时,S△F1PF2 =
,由此能求出S△F1PF2=b1b2.
(2)当b1+b2=m时,有m=b1+b2≥2
,由此能求出面积的最大值是
.
| sinθ |
| 1+cosθ |
| b22sinθ |
| 1-cosθ |
(2)当b1+b2=m时,有m=b1+b2≥2
| b1b2 |
| m2 |
| 4 |
解答:
解:(1)设∠F1PF2=θ,当PF1+PF2=2a1时,
F1F22=PF12+PF22-2PF1•PF2cosθ,
即2PF1•PF2cosθ=(PF1+PF2)2-2PF1•PF2-4c2=4a12-2PF1•PF2-4c2,
∴PF1•PF2=
,
∴S△F1PF2=
×PF1•PF2sinθ=b12•
,
当PF1-PF2=2a2时,
F1F22=PF12+PF22-2PF1•PF2cosθ,
即2PF1•PF2cosθ=(PF1-PF2)2+2PF1•PF2-4c2=4a22+2PF1•PF2-4c2,
∴PF1•PF2=
,
∴S△F1PF2 =
×PF1•PF2sinθ=
,
(S△F1PF2)2=
×
=b12•b22,
∴S△F1PF2=b1b2.
(2)当b1+b2=m时,有m=b1+b2≥2
,
即有b1b2≤
,△F1PF的面积S△F1PF2 ≤
.
即面积的最大值是
.
F1F22=PF12+PF22-2PF1•PF2cosθ,
即2PF1•PF2cosθ=(PF1+PF2)2-2PF1•PF2-4c2=4a12-2PF1•PF2-4c2,
∴PF1•PF2=
| 2b12 |
| 1+cosθ |
∴S△F1PF2=
| 1 |
| 2 |
| sinθ |
| 1+cosθ |
当PF1-PF2=2a2时,
F1F22=PF12+PF22-2PF1•PF2cosθ,
即2PF1•PF2cosθ=(PF1-PF2)2+2PF1•PF2-4c2=4a22+2PF1•PF2-4c2,
∴PF1•PF2=
| 2b22 |
| 1-cosθ |
∴S△F1PF2 =
| 1 |
| 2 |
| b22sinθ |
| 1-cosθ |
(S△F1PF2)2=
| b12sinθ |
| 1+cosθ |
| b22sinθ |
| 1-cosθ |
∴S△F1PF2=b1b2.
(2)当b1+b2=m时,有m=b1+b2≥2
| b1b2 |
即有b1b2≤
| m2 |
| 4 |
| m2 |
| 4 |
即面积的最大值是
| m2 |
| 4 |
点评:本题考查三角形面积的表示和面积最大值的求法,解题时要认真审题,注意双曲线和椭圆的简单性质的灵活运用.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,且a1=2,若数列{Sn}也为等差数列,则S2014=( )
| A、1007 | B、2014 |
| C、4028 | D、0 |
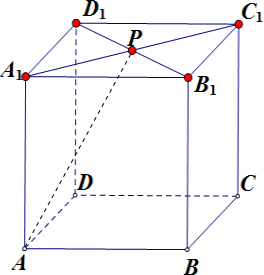 在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.
在一个正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1的中心,求证AP⊥PB1.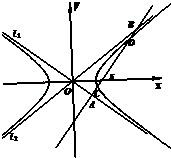 双曲线
双曲线