题目内容
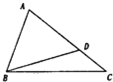如图，在△ABC中，sin| ∠ABC |
| 2 |
| ||
| 3 |
4
| ||
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：利用二倍角的余弦函数公式即可求出cos∠ABC的值，设BC=a，AC=3b，由AD=2DC得到AD=2b，DC=b，在三角形ABC中，利用余弦定理得到关于a与b的关系式，在三角形ABD和三角形DBC中，利用余弦定理分别表示出cos∠ADB和cos∠BDC，由于两角互补，得到cos∠ADB等于-cos∠BDC，两个关系式互为相反数，得到a与b的另一个关系式，求出a．，b即可得到结论．
解答：
解：因为sin
=
，所以cos∠ABC=1-2sin2
=1-2×（
）2=1-2×
=
，
在△ABC中，设BC=a，AC=3b，
由余弦定理可得9b2=a2+4-
a：①
在△ABD和△DBC中，由余弦定理可得：cos∠ADB=
，
cos∠BDC=
，
因为cos∠ADB=-cos∠BDC，所以有
-
，
所以3b2-a2=-6 ②
由①②可得a=3，b=1，即BC=3，AC=3．
则cosC=
=
=
，
故答案为：
| ∠ABC |
| 2 |
| ||
| 3 |
| ∠ABC |
| 2 |
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
在△ABC中，设BC=a，AC=3b，
由余弦定理可得9b2=a2+4-
| 4 |
| 3 |
在△ABD和△DBC中，由余弦定理可得：cos∠ADB=
4b2+
| ||||
|
cos∠BDC=
b2+
| ||||
|
因为cos∠ADB=-cos∠BDC，所以有
4b2+
| ||||
|
b2+
| ||||
|
所以3b2-a2=-6 ②
由①②可得a=3，b=1，即BC=3，AC=3．
则cosC=
| AC2+BC2-AB2 |
| 2AC•BC |
| 32+32-22 |
| 2×3×3 |
| 7 |
| 9 |
故答案为：
| 7 |
| 9 |
点评：本题主要考查余弦定理和正弦定理的应用，考查学生灵活运用同角三角函数间的基本关系及余弦定理化简求值，有一定的难度．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
若不等式x2-px+q=0的解集为（-
，
），则不等式qx2+px+1＞0的解集为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、（-3，2） | ||||
| B、（-2，3） | ||||
C、（-
| ||||
D、（-
|
已知函数f（x）的导函数的图象如图所示，则下列判断中正确的是（ ）
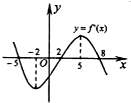
| A、函数f（x）在区间（-2，2）内单调递增 |
| B、函数f（x）在区间（-5，2）内单调递减 |
| C、函数f（x）在区间（5，8）内单调递减 |
| D、函数f（x）在区间（-2，5）内为单调函数 |