题目内容
已知
，求n-2m的最大值．
|
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：由约束条件作出可行域，令t=n-2m，联立
，消去n后由判别式等于0求得答案．
|
解答：
解：由约束条件
作出可行域如图，
令t=n-2m，则n=2m+t，
联立
，消去m得：4n2-n+t=0．
由△=（-1）2-16t=0，得t=
．
∴n-2m的最大值为
．
故答案为：
．
|
令t=n-2m，则n=2m+t，
联立
|
由△=（-1）2-16t=0，得t=
| 1 |
| 16 |
∴n-2m的最大值为
| 1 |
| 16 |
故答案为：
| 1 |
| 16 |
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
下列函数与y=|x|表示同一个函数的是（ ）
A、y=（
| ||||||
B、y=（
| ||||||
C、y=（
| ||||||
D、y=
|
“m=-1”是“直线mx+（2m-1）y+1=0，和直线3x+my+9=0垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设f（x）是定义在R上的函数，f（0）=2，对任意x∈R，f（x）+f′（x）＞1，则不等式exf（x）＞ex+1的解集为（ ）
| A、（0，+∞） |
| B、（-∞，0） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，-1）∪（0，1） |
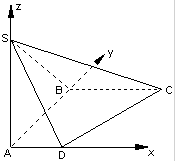已知ABCD为直角梯形，∠DAB=∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=