题目内容
设f(x)是定义在R上的函数,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1的解集为( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:本题构造新函数g(x)=exf(x)-ex,利用条件f(x)+f’(x)>1,得到g′(x)>0,得到函数g(x)单调递增,再利用f(0)=2,得到函数g(x)过定点(0,1),解不等式exf(x)>ex+1,即研究g(x)>1,结合函数的图象,得到x的取值范围,即本题结论.
解答:
解:令g(x)=exf(x)-ex,
则g′(x)=exf(x)+exf′(x)-ex,
∵对任意x∈R,f(x)+f′(x)>1,
∴g′(x)=ex[f(x)+f′(x)-1]>0,
∴函数y=g(x)在R上单调递增.
∵f(0)=2,
∴g(0)=1.
∴当x<0时,g(x)<1;
当x>0时,g(x)>1.
∵exf(x)>ex+1,
∴exf(x)-ex>1,
即g(x)>1,
∴x>0.
故选A.
则g′(x)=exf(x)+exf′(x)-ex,
∵对任意x∈R,f(x)+f′(x)>1,
∴g′(x)=ex[f(x)+f′(x)-1]>0,
∴函数y=g(x)在R上单调递增.
∵f(0)=2,
∴g(0)=1.
∴当x<0时,g(x)<1;
当x>0时,g(x)>1.
∵exf(x)>ex+1,
∴exf(x)-ex>1,
即g(x)>1,
∴x>0.
故选A.
点评:本题考查了函数的导数与单调性,还考查了构造法思想,本题有一定的难度,计算量适中,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
f(x)是定义在R上的奇函数且x>0时,f(x)=2x2-x+3,则当x<0时,f(x)的解析式为( )
| A、2x2-x+3 |
| B、-2x2+x-3 |
| C、2x2+x+3 |
| D、-2x2-x-3 |
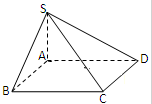 在四棱锥S-ABCD中,∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小.
在四棱锥S-ABCD中,∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小. 已知三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=90°,∠ACB=45°,CC1=2AC=4,D为CC1中点.
已知三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=90°,∠ACB=45°,CC1=2AC=4,D为CC1中点.