题目内容
在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为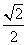 ,设动点P的轨迹为C.
,设动点P的轨迹为C.
(1)求出轨迹C的方程;
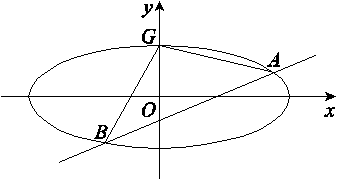
(2)设动直线l:y=kx-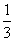 与曲线C交于A,B两点,问在y轴上是否存在定点G,使∠AGB为直角?若存在,求出G的坐标,并求△AGB面积的最大值;若不存在,请说明理由.
与曲线C交于A,B两点,问在y轴上是否存在定点G,使∠AGB为直角?若存在,求出G的坐标,并求△AGB面积的最大值;若不存在,请说明理由.
解:(1)设P(x,y),则依题意有
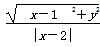 =
=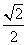 ,化简得
,化简得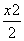 +y2=1.
+y2=1.
(2)由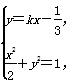 得
得
(2k2+1)x2-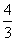 kx-
kx-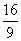 =0.
=0.
设A(x1,y1),B(x2,y2),G(0,m),
 则需
则需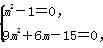 解得m=1.
解得m=1.
因此,存在点G(0,1),使得∠AGB为直角.
又点G到AB的距离d=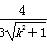
所以,S△AGB=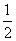 |AB|d=
|AB|d=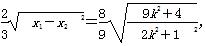 ,
,
设t=2k2+1,t∈[1,+∞),
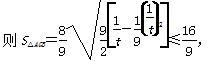 当且仅当t=1时,上式等号成立.
当且仅当t=1时,上式等号成立.
因此,△AGB 面积的最大值是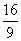 .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 中,
中, 分别为
分别为 的中点,则
的中点,则 与
与 所成的角的大小为
所成的角的大小为 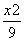 -
-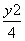 =1上的点.P是线段P1P2的中点,直线OP,P1P2的斜率分别为k1,k2,若2≤k1≤4,则k2的取值范围是( )
=1上的点.P是线段P1P2的中点,直线OP,P1P2的斜率分别为k1,k2,若2≤k1≤4,则k2的取值范围是( )

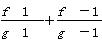 =
=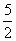 .若数列
.若数列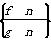 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )


 dx=________.
dx=________. 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 等于( )
等于( ) D、
D、