题目内容
定义在R上的函数f(x)满足：f(x)＋f′(x)>1，f(0)＝4，则不等式exf(x)>ex＋3(其中e为自然对数的底数)的解集为( )
A．(0，＋∞) B．(－∞，0)∪(3，＋∞)
C．(－∞，0)∪(0，＋∞) D．(3，＋∞)
A
[解析] 令F(x)＝exf(x)－ex－3，则F′(x)＝exf(x)＋exf′(x)－ex＝ex(f(x)＋f′(x)－1)>0，∴函数F(x)＝exf(x)－ex－3在R上单调递增．又F(0)＝0，∴F(x)＝exf(x)－ex－3>0的解集为(0，＋∞)，即不等式exf(x)>ex＋3(其中ex为自然对数的底数)的解集为(0，＋∞)．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，
，则“
”是“
”的（ ）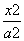
－
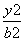＝1(a>0，b>0)的左焦点，离心率为e，过F且平行于双曲线渐近线的直线与圆x2＋y2＝c2交于点P，且点P在抛物线y2＝4cx上，则e2等于( )
B.
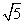
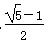D.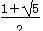
－
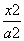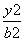＝1(a>0，b>0)的左、右焦点，P为双曲线上一点，若∠F1PF2＝90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是( )
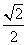，设动点P的轨迹为C.
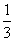与曲线C交于A，B两点，问在y轴上是否存在定点G，使∠AGB为直角？若存在，求出G的坐标，并求△AGB面积的最大值；若不存在，请说明理由．
的图象在点(－1,2)处的切线与坐标轴围成的三角形的面积等于( )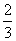
B.
C.
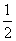D.
(0<x<1)图象上一点M作切线l与y轴和直线y＝1分别交于点P，Q，点N(0,1)，则△PQN面积的最大值为________．
的最大值为 。