题目内容
已知f(x)，g(x)都是定义在R上的函数，g(x)≠0，f′(x)g(x)>f(x)g′(x)，且f(x)＝axg(x)(a>0且a≠1)，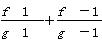
＝
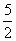.若数列
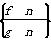的前n项和大于62，则n的最小值为( )
A．6 B．7 C．8 D．9
A
[解析] ∵f(x)＝axg(x)(a>0，且a≠1)，
∴
＝ax.
又∵f′(x)·g(x)>f(x)g′(x)，
∴
′＝
>0，
∴＝ax是增函数，∴a>1.∵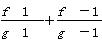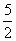＝，∴a＋a－1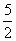＝，解得a＝2或a＝
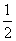(舍)，∴数列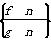为{2n}．∵数列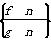的前n项和大于62，∴2＋22＋23＋…＋2n＝
＝2n＋1－2>62，即2n＋1>64＝26，
∴n>5，∴n的最小值为6，故选A.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
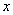表示某学科知识的学习次数（
），
表示对该学科知识的掌握程度，正实数a与学科知识有关
7时，掌握程度的增长量f（x+1）- f(x)总是下降；
，掌握程度是85%，请确定相应的学科.
＋
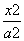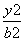＝1(a>b>0)的左焦点为F，右顶点为A，上顶点为B，O为坐标原点，M为椭圆上任意一点，过F，B，A三点的圆的圆心坐标为(p，q)．
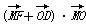的最小值为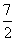
，求椭圆的方程．
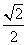，设动点P的轨迹为C.
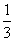与曲线C交于A，B两点，问在y轴上是否存在定点G，使∠AGB为直角？若存在，求出G的坐标，并求△AGB面积的最大值；若不存在，请说明理由．
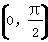上不是凸函数的是( )
>0，则函数F(x)＝xf(x)＋
的零点个数是( )
中随机地取两个数，则这两个数之和大于1的概率是（ ）
B．
C．
D．