题目内容
2.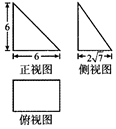 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
分析 如图所示的四棱锥P-ABCD,其中PA⊥ABCD,ABCD为正方形.补成以AB,AD,AP为相邻的三条棱的长方体,可得该阳马的外接球的直径为长方体的对角线.
解答 解:如图所示的四棱锥P-ABCD,其中PA⊥ABCD,ABCD为正方形.
补成以AB,AD,AP为相邻的三条棱的长方体,可得该阳马的外接球的直径为长方体的对角线.
则该阳马的外接球的直径=$\sqrt{{6}^{2}+{6}^{2}+(2\sqrt{7})^{2}}$=10.
∴该阳马的外接球的表面积=$4π×(\frac{10}{2})^{2}$=100πcm2.
故选:A.
点评 本题考查了正方体长方体与四棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.下列参数方程中表示直线x+y-2=0的是( )
| A. | $\left\{\begin{array}{l}x=2+t\\ y=1-t\end{array}\right.(t$为参数) | B. | $\left\{\begin{array}{l}x=1-\sqrt{t}\\ y=1+\sqrt{t}\end{array}\right.(t$为参数) | ||
| C. | $\left\{\begin{array}{l}x=3+t\\ y=-1-t\end{array}\right.(t$为参数) | D. | $\left\{\begin{array}{l}x=1-{t^2}\\ y=1+{t^2}\end{array}\right.(t$为参数) |
10.已知两组数据x,y的对应值如下表,若已知x,y是线性相关的且线性回归方程为:$\hat y=\hat bx+\hat a$,经计算知:$\hat b=-1.4$,则$\hat a$=( )
| x | 4 | 5 | 6 | 7 | 8 |
| y | 12 | 10 | 9 | 8 | 6 |
| A. | -0.6 | B. | 0.6 | C. | -17.4 | D. | 17.4 |