题目内容

12．下面几种推理是合情推理的是①②④
①由圆的性质类比出球的有关性质；
②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；
③教室内有一把椅子坏了，则该教室内的所有椅子都坏了；
④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得出凸多边形的内角和是（n-2）•180°．

分析 根据题意，依次分析所给的推理，是否符合合情推理的定义，综合即可得答案．

解答 解：根据题意，依次分析4个推理：
对于①、在推理过程由圆的性质类比出球的有关性质，是类比推理；
对于②、符合归纳推理的定义，即是由特殊到一般的推理过程，是归纳推理；
对于③、不是合情推理，
对于④、符合归纳推理的定义，即是由特殊到一般的推理过程，是归纳推理；
则是合情推理的是①②④；
故答案为：①②④．

点评 本题考查合情推理的定义，关键是理解合情推理的定义、分类以及归纳推理与类比推理的定义．

练习册系列答案
相关题目
14．在区间（0，5）内任取一个实数m，则满足3＜m＜4的概率为$\frac{1}{5}$．
3．已知数列{an}的前n项和为Sn，点（n，Sn+3）（n∈N*）在函数y=3×2x的图象上，等比数列{bn}满足bn+bn+1=an（n∈N*）．其前n项和为Tn，则下列结论正确的是（　　）
A．Sn=2TnB．Tn=2bn+1C．Tn＞anD．Tn＜bn+1
20．已知函数f（x）=$\frac{1}{2}$x2-x+alnx（a＞0）有两个极值点x1、x2，且x1＜x2．
（1）求a的取值范围；
（2）证明：f（x1）+f（x2）＞$\frac{-3-2ln2}{4}$．
7．已知a为实数，且函数f（x）=（x2-4）（x-a），f'（-1）=0．
（1）求函数f（x）的单调区间；
（2）求函数f（x）在[-2，2]上的最大值、最小值．
17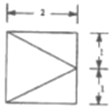．己知四梭锥．它的底面是边长为2的正方形．其俯视图如图所示，左视图为直角三角形，则四棱锥的外接球的表面枳为（　　）
A．8πB．12πC．4πD．16π
4．在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴，取相同的单位长度，建立极坐标系，已知曲线C1的参数方程为$\left\{\begin{array}{l}x=sinα\\ y=cos2α\end{array}\right.$，（$α∈[{0，\frac{π}{2}}]$，α为参数），曲线C2的极坐标方程为$θ=-\frac{π}{6}$，求曲线C1与曲线C2的交点的直角坐标．
1．某校举行高二理科学生的数学与物理竞赛，并从中抽取72名学生进行成绩分析，所得学生的及格情况统计如表：
物理及格物理不及格合计
数学及格28836
数学不及格162036
合计442872
（1）根据表中数据，判断是否是99%的把握认为“数学及格与物理及格有关”；
（2）若以抽取样本的频率为概率，现在该校高二理科学生中，从数学及格的学生中随机抽取3人，记X为这3人中物理不及格的人数，从数学不及格学生中随机抽取2人，记Y为这2人中物理不及格的人数，记ξ=|X-Y|，求ξ的分布列及数学期望．
附：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{21}{n}_{12}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$．
P（X2≥k）0.1500.1000.0500.010
k2.0722.7063.8416.635
8．某四棱锥的三视图如图所示，则最长的一条侧棱的长度是（　　）
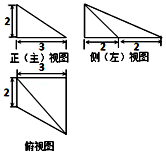
A．$2\sqrt{5}$B．$4\sqrt{2}$C．$\sqrt{29}$D．$\sqrt{13}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网