题目内容
5.在平面直角坐标系中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的参数方程为$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}\right.$(α为参数,α∈[0,π]),直线l的极坐标方程为$ρ=\frac{4}{{\sqrt{2}sin({θ-\frac{π}{4}})}}$.(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)P为曲线C上任意一点,Q为直线l任意一点,求|PQ|的最小值.
分析 (1)曲线C的参数方程消去参数α,能求出曲线C的普通方程;直线l的极坐标方程转化为ρsinθ-ρcosθ=4,由此能求出直线l的直角坐标方程.
(2)设P(1+cosα,sinα),α∈[0,π]),求出P到直线l的距离,结合三角函数的性质能求出|PQ|的最小值.
解答 解:(1)∵曲线C的参数方程为$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}\right.$(α为参数,α∈[0,π]),
∴曲线C的普通方程为(x-1)2+y2=1.(y≥0).
∵直线l的极坐标方程为$ρ=\frac{4}{{\sqrt{2}sin({θ-\frac{π}{4}})}}$,
即ρsinθ-ρcosθ=4,
∴直线l的直角坐标方程为x-y+4=0.
(2)∵P为曲线C上任意一点,Q为直线l任意一点,
∴设P(1+cosα,sinα),α∈[0,π],
则P到直线l的距离:
d=$\frac{|1+cosα-sinα+4|}{\sqrt{2}}$=$\frac{|\sqrt{2}sin(α+\frac{3π}{4})+5|}{\sqrt{2}}$,
∵α∈[0,π],∴当α=$\frac{3π}{4}$时,dmin=$\frac{5-\sqrt{2}}{\sqrt{2}}$=$\frac{5\sqrt{2}-2}{2}$.
∴|PQ|的最小值为$\frac{5\sqrt{2}-2}{2}$.
点评 本题考查曲线的普通方程和直线的直角坐标方程的求法,考查线段长的最小值的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
13.下列参数方程中表示直线x+y-2=0的是( )
| A. | $\left\{\begin{array}{l}x=2+t\\ y=1-t\end{array}\right.(t$为参数) | B. | $\left\{\begin{array}{l}x=1-\sqrt{t}\\ y=1+\sqrt{t}\end{array}\right.(t$为参数) | ||
| C. | $\left\{\begin{array}{l}x=3+t\\ y=-1-t\end{array}\right.(t$为参数) | D. | $\left\{\begin{array}{l}x=1-{t^2}\\ y=1+{t^2}\end{array}\right.(t$为参数) |
20.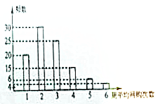 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
(2)若从网购迷中任意选取2名,求其中年龄丑啊过40岁的市民人数ξ的分布列与期望.
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$;
 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$;
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
10.已知两组数据x,y的对应值如下表,若已知x,y是线性相关的且线性回归方程为:$\hat y=\hat bx+\hat a$,经计算知:$\hat b=-1.4$,则$\hat a$=( )
| x | 4 | 5 | 6 | 7 | 8 |
| y | 12 | 10 | 9 | 8 | 6 |
| A. | -0.6 | B. | 0.6 | C. | -17.4 | D. | 17.4 |
3.已知数列{an}的前n项和为Sn,点(n,Sn+3)(n∈N*)在函数y=3×2x的图象上,等比数列{bn}满足bn+bn+1=an(n∈N*).其前n项和为Tn,则下列结论正确的是( )
| A. | Sn=2Tn | B. | Tn=2bn+1 | C. | Tn>an | D. | Tn<bn+1 |