题目内容

2．圆心为（1，2），且与y轴相切的圆的方程是（　　）
A．（x+1）2+（y+2）2=4B．（x-1）2+（y-2）2=4C．（x+1）2+（y+2）2=1D．（x-1）2+（y-2）2=1

分析 由所求圆与y轴相切，得到圆心的横坐标的绝对值为圆的半径，进而由圆心C的坐标和求出的半径写出圆的标准方程即可

解答 解：∵圆心C的坐标为（1，2），且所求圆与y轴相切，
∴圆的半径r=1，
则所求圆的方程为（x-1）2+（y-2）2=1．
故选：D．

点评 此题考查了直线与圆的位置关系，涉及的知识有：圆的标准方程，点到直线的距离公式，当直线与圆相切时，圆心到直线的距离等于圆的半径，其中根据题意得到圆心横坐标的绝对值为圆的半径是解本题的关键．

练习册系列答案
相关题目
7．△ABC中，a：b：c=2：$\sqrt{6}$：（$\sqrt{3}$+1），则最大角的余弦值为$\frac{\sqrt{6}-\sqrt{2}}{4}$．
8．已知sinx=2cosx，则$\frac{si{n}^{2}x}{1+co{s}^{2}x}$=$\frac{2}{3}$．
10．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=$\sqrt{3}$，且|$\overrightarrow{a}$-2$\overrightarrow{b}$|=1，则$\overrightarrow{a}$•$\overrightarrow{b}$=5．
17．已知命题P：x1，x2是方程x2-mx-1=0的两个实根，且不等式a2+4a-3≤|x1-x2|对任意m∈R恒成立；命题q：不等式ax2+2x-1＞0有解，若命题p∨q为真，p∧q为假，求实数a的取值范围．
7．已知四棱锥P-ABCD如图（1），它的三视图如图（2）所示，其中PA⊥平面ABCD，△PBC为正三角形．

（1）求证：AC⊥平面PAB；
（2）求点A到平面PBC的距离．
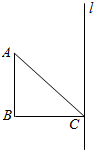14．如图，三角形ABC是等腰直角三角形，∠B=90°，AB=1，直线l经过点C且与AB平行，将三角形ABC绕直线l旋转一周得到一个几何体．
（1）求几何体的表面积；
（2）求几何体的体积．
11．集合A={x|0＜x2-x-2≤10}，集合$B=\{x|\frac{1}{x+2}＞0\}$，求A∩B．
12．不等式（ax-2）（x-1）≥0（a＜0）的解集为（　　）
A．[$\frac{2}{a}$，1]B．[1，$\frac{2}{a}$）C．（-∞，$\frac{2}{a}$]∪[1，+∞）D．（-∞，1]∪[$\frac{2}{a}$，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网