题目内容
12．不等式（ax-2）（x-1）≥0（a＜0）的解集为（ ）| A． | [$\frac{2}{a}$，1] | B． | [1，$\frac{2}{a}$） | C． | （-∞，$\frac{2}{a}$]∪[1，+∞） | D． | （-∞，1]∪[$\frac{2}{a}$，+∞） |
分析 先求出方程的根，结合a的符号，从而求出不等式的解集即可．
解答 解：令（ax-2）（x-1）=0，
解得：x=1或x=$\frac{2}{a}$，
由a＜0，得：$\frac{2}{a}$＜x＜1，
故选：A．
点评 本题考察了解不等式问题，是一道基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2．圆心为（1，2），且与y轴相切的圆的方程是（ ）
| A． | （x+1）2+（y+2）2=4 | B． | （x-1）2+（y-2）2=4 | C． | （x+1）2+（y+2）2=1 | D． | （x-1）2+（y-2）2=1 |
3．
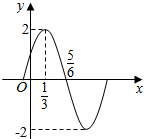已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）| A． | f（x）=2sin（πx+$\frac{π}{6}$） | B． | f（x）=2sin（πx+$\frac{π}{3}$） | C． | $f（x）=2sin（{2πx-\frac{π}{6}}）$ | D． | y=2sin（πx-$\frac{π}{6}$） |
7．棱长为2的正四面体的表面积是（ ）
| A． | 4$\sqrt{3}$ | B． | 4 | C． | $\sqrt{3}$ | D． | 16 |
4．在由一组样本数据（x1，y1），（x2，y2），…，（xn，yn）（n≥2，x1，x2，…，xn不全相等）的点所构成的散点图中，若所有样本点（xi，yi）（i=1，2，…，n）都在直线y=-2x+1上，则这组样本数据中变量x，y的相关系数为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
2．设f（x）=2+5x+10x2+10x3+5x4+x5，则其反函数的解析式为（ ）
| A． | $y=1+\root{5}{x-1}$ | B． | $y=1-\root{5}{x-1}$ | C． | $y=-1+\root{5}{x-1}$ | D． | $y=-1-\root{5}{x-1}$ |