Question

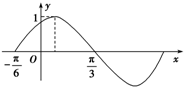函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜

π

2

）的部分图象如图所示，如果x₁，x₂∈（-

π

6

，

π

3

），且f（x₁）=f（x₂），则f（x₁+x₂）=（　　）

• A、

  1

  2

• B、

  2

  2

• C、1
• D、

  3

  2

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：通过函数的图象求出函数的周期，利用函数的图象经过的特殊点求出函数的初相，得到函数的解析式，利用函数的图象与函数的对称性求出f（x₁+x₂）即可．

解答： 解：由图知，T=2×（

π

3

+

π

6

）=π，
∴ω=2，因为函数的图象经过（-

π

6

），0=sin（-

π

3

+φ）
∵|φ|＜

π

2

，所以φ=

π

3

，
∴f（x）=sin（2x+

π

3

），x₁+x₂=2×

π

12

=

π

6

，
所以f（x₁+x₂）=sin

2π

3

=

3

2

．
故选：D．

点评：本题考查三角函数的解析式的求法，函数的图象的应用，函数的对称性，考查计算能力，属于中档题．