题目内容
关于函数f(x)=sin(-2x+
),给出以下四个论断
①函数图象关于直线x=-
对称;
②函数图象一个对称中心是(
,0);
③函数f(x)在区间[-
,
]上是减函数;
④当且仅当kπ+
<x<kπ+
(k∈Z)时,f(x)<0.
以上四个论断正确的序号是 .
| π |
| 4 |
①函数图象关于直线x=-
| 5π |
| 8 |
②函数图象一个对称中心是(
| 7π |
| 8 |
③函数f(x)在区间[-
| π |
| 8 |
| 3π |
| 8 |
④当且仅当kπ+
| 5π |
| 8 |
| 7π |
| 8 |
以上四个论断正确的序号是
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:①求出对称轴x=-
-
,k∈Z,当k=1时,有x=-
,故命题正确;
②求出对称中心横坐标x=
-
,k∈Z,比较判断即可;
③求出函数y=sin(-2x+
)的单调递减区间为[kπ-
,kπ+
],k∈z.故命题正确;
④取特殊值x=
时,f(x)<0且x不属于[kπ+
,kπ+
],(k∈Z).故命题不正确;
| kπ |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
②求出对称中心横坐标x=
| π |
| 8 |
| kπ |
| 2 |
③求出函数y=sin(-2x+
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
④取特殊值x=
| π |
| 2 |
| 5π |
| 8 |
| 7π |
| 8 |
解答:
解:①因为-2x+
=kπ+
,可解得x=-
-
,k∈Z,当k=1时,有x=-
,故命题正确;
②因为-2x+
=kπ,可解得x=
-
,k∈Z,故命题不正确;
③由 2kπ-
≤2x-
≤2kπ+
,k∈z,可得 kπ-
≤x≤kπ+
,k∈z,故函数y=sin(-2x+
)的单调递减区间为[kπ-
,kπ+
],k∈z.故命题正确;
④当x=
时,f(x)<0且x不属于[kπ+
,kπ+
],(k∈Z).故命题不正确;
故答案为:①③.
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
②因为-2x+
| π |
| 4 |
| π |
| 8 |
| kπ |
| 2 |
③由 2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
④当x=
| π |
| 2 |
| 5π |
| 8 |
| 7π |
| 8 |
故答案为:①③.
点评:本题主要考察正弦函数的图象和性质,考察计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若点P(a,1)在椭圆
+
=1的外部,则a的取值范围是( )
| x2 |
| 2 |
| y2 |
| 3 |
A、(-
| ||||||||
B、(-∞,-
| ||||||||
C、(
| ||||||||
D、(-∞,-
|
设x>0,y>0,x+y=1,则
+
≤a恒成立的a的最小值是( )
| x |
| y |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
设f(x)=
x3+ax2+5x+6在区间[1,3]上为单调递减函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、(-∞,-
| ||||
| B、(-∞,-3] | ||||
C、(-∞,-3]∪[-
| ||||
D、(-
|
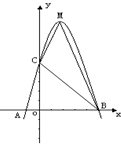 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.