题目内容
2.已知函数f(x)=lg(x2-x-2)的定义域为集合A,函数$g(x)={x^{\frac{1}{2}}}$,x∈[0,9]的值域为集合B,(1)求A∩B;
(2)若C={x|3x<2m-1},且(A∩B)⊆C,求实数m的取值范围.
分析 (1)由对数函数的定义域求出集合A,由函数$g(x)={x^{\frac{1}{2}}}$,x∈[0,9]的值域求出集合B,则A∩B可求;
(2)由集合C化为$C=\left\{{x|x<\frac{2m-1}{3}}\right\}$且(A∩B)⊆C得到不等式$\frac{2m-1}{3}>3$,求解不等式即可得到实数m的取值范围.
解答 解:(1)已知函数f(x)=lg(x2-x-2)的定义域为集合A,函数$g(x)={x^{\frac{1}{2}}}$,x∈[0,9]的值域为集合B,
则A={x|x2-x-2>0}={x|x<-1或x>2},B={x|0≤x≤3},
∴A∩B={x|x<-1或x>2}∩{x|0≤x≤3}={x|2<x≤3};
(2)∵$C=\left\{{x|x<\frac{2m-1}{3}}\right\}$且(A∩B)⊆C,
∴$\frac{2m-1}{3}>3$,即m>5.
点评 本题考查了集合的包含关系判断及应用,考查了函数的定义域及值域的求法,考查了交集及其运算,是中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
12.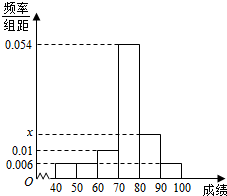 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )| A. | 75.5 | B. | 75.2 | C. | 75.1 | D. | 75.3 |
17.在△ABC中,已知D是BC延长线上一点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,点E为线段AD的中点,$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}\overrightarrow{AC}$,则λ=( )
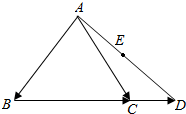

| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
7.三张奖券中有2张是有奖的,甲、乙两人从中各抽一张(抽出后不放回),甲先抽,然后乙抽,设甲中奖的概率为P1,乙中奖的概率为P2,那么( )
| A. | P1=P2 | B. | P1<P2 | ||
| C. | P1>P2 | D. | P1,P2的大小无法确定 |
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )
| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
11.设l,m,n是三条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
| A. | α∥β,l?α,n?β⇒l∥n | B. | l⊥n,l⊥α⇒n∥α | C. | l⊥α,l∥β⇒α⊥β | D. | α⊥β,l?α⇒l⊥β |
12.已知p:m∈(-2,-1),q:m满足$\frac{{x}^{2}}{2+m}-\frac{{y}^{2}}{m+1}=1$表示椭圆,那么p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
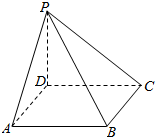 已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.