题目内容
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且$\sqrt{3}$asinB-bcosA=b.(1)求A;
(2)若b+c=2,当a取最小值时,求△ABC的面积.
分析 (1)由题意和正弦定理可得sin(A-$\frac{π}{6}$)=$\frac{1}{2}$,结合三角形内角的范围可得角A;
(2)由余弦定理可得a2=4-3bc,再由已知式子和基本不等式可得bc的范围,可得此时边长,可得三角形的面积.
解答 解:(1)∵在△ABC中$\sqrt{3}$asinB-bcosA=b,
∴由正弦定理可得$\sqrt{3}$sinAsinB-sinBcosA=sinB,
由三角形内角的范围可得sinB≠0,
∴约掉sinB可得$\sqrt{3}$sinA-cosA=1,
∴2sin(A-$\frac{π}{6}$)=1,即sin(A-$\frac{π}{6}$)=$\frac{1}{2}$,
∴A-$\frac{π}{6}$=$\frac{π}{6}$或$\frac{5π}{6}$,解得A=$\frac{π}{3}$,或A=π(舍去),
故A=$\frac{π}{3}$;
(2)由余弦定理可得a2=b2+c2-2bccosA
=b2+c2-bc=(b+c)2-3bc=4-3bc,
由基本不等式可得bc≤($\frac{b+c}{2}$)2=1,当且仅当b=c=1时取等号,
故-bc≥-1,∴-3bc≥-3,故a2=4-3bc≥1,
∴a的最小值为1,此时△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$.
点评 本题考查正余弦定理解三角形,涉及基本不等式求最值和和差角的三角函数公式,属中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
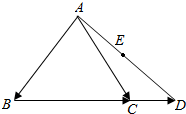
17.在△ABC中,已知D是BC延长线上一点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,点E为线段AD的中点,$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}\overrightarrow{AC}$,则λ=( )

| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )
| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
1.一个直四棱柱的侧棱长等于2,底面是边长为1的正方形,如果其俯视图是一个面积为1的正方形,其侧视图的面积的取值范围是( )
| A. | [1,2] | B. | [2,2$\sqrt{2}$] | C. | [1,2$\sqrt{2}$] | D. | [$\sqrt{3}$,2$\sqrt{2}$] |
11.设l,m,n是三条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
| A. | α∥β,l?α,n?β⇒l∥n | B. | l⊥n,l⊥α⇒n∥α | C. | l⊥α,l∥β⇒α⊥β | D. | α⊥β,l?α⇒l⊥β |
15.已知双曲线my2-x2=1(m∈R)与抛物线x2=8y有相同的焦点,则该双曲线的渐近线方程为( )
| A. | y=±$\sqrt{3}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
16.已知数列{an}为等差数列,且a3+a5+a10+a12=64,则a7+a8=( )
| A. | 16 | B. | 64 | C. | 24 | D. | 32 |