题目内容
5.已知全集U=R,集合A={x|($\frac{1}{2}$)x≤1,B={x|x2-6x+8≤0},则A∩B为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
分析 分别求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.
解答 解:由A中不等式变形得:($\frac{1}{2}$)x≤1=($\frac{1}{2}$)0,即x≥0,
∴A={x|x≥0},
由B中方程变形得:(x-2)(x-4)≤0,
解得:2≤x≤4,即B={x|2≤x≤4},
则A∩B={x|2≤x≤4},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
17.在△ABC中,已知D是BC延长线上一点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,点E为线段AD的中点,$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}\overrightarrow{AC}$,则λ=( )
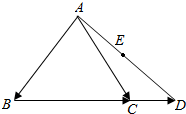

| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )
| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
15.已知双曲线my2-x2=1(m∈R)与抛物线x2=8y有相同的焦点,则该双曲线的渐近线方程为( )
| A. | y=±$\sqrt{3}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
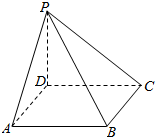 已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.