在△ABC中.∠C=$\frac{π}{6}$.AC=2$\sqrt{3}$.AB=2.则BC的长是( )A．2B．4C．2或4D．4或8 题目和参考答案——青夏教育精英家教网—

题目内容

9．在△ABC中，∠C=$\frac{π}{6}$，AC=2$\sqrt{3}$，AB=2，则BC的长是（　　）

A．

B．

C．

2或4

D．

4或8

分析由已知利用余弦定理即可解得BC的值．

解答解：∵∠C=$\frac{π}{6}$，AC=2$\sqrt{3}$，AB=2，
∴由余弦定理可得：AB²=AC²+BC²-2•AC•BC•cosC=（2$\sqrt{3}$）²+BC²-2×$2\sqrt{3}×BC×\frac{\sqrt{3}}{2}$=4，
∴整理可得：BC²-6BC+8=0，解得：BC=2或4．
故选：C．

点评本题主要考查了余弦定理在解三角形中的应用，属于基础题．

练习册系列答案

20．下列结论中：
①函数$y=x（1-2x）（0＜x＜\frac{1}{2}）$有最大值为$\frac{1}{8}$；
②函数y=2-3x-$\frac{4}{x}$（x＜0）有最大值2-4$\sqrt{3}$；
③若a＞0，则$（1+a）（1+\frac{1}{a}）≥4$．
正确的序号为①③．

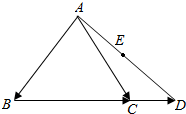
17．在△ABC中，已知D是BC延长线上一点，若$\overrightarrow{BC}$=2$\overrightarrow{CD}$，点E为线段AD的中点，$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}\overrightarrow{AC}$，则λ=（　　）

4．已知函数$f（x）=\frac{a}{{{a^2}-1}}（{a^x}-{a^{-x}}）\;（a＞0且a≠1）$．
（1）判断f（x）的奇偶性；
（2）当x∈[-1，1]时，f（x）≥m恒成立，求m的取值范围．

14．已知x∈（0，π），且$cos（x-\frac{π}{4}）=\frac{1}{3}$，则tanx=（　　）

	A．	$-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$		B．	$-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$
	C．	$-\frac{{9+4\sqrt{2}}}{7}$		D．	$-\frac{{9-4\sqrt{2}}}{7}$

1．一个直四棱柱的侧棱长等于2，底面是边长为1的正方形，如果其俯视图是一个面积为1的正方形，其侧视图的面积的取值范围是（　　）

[$\sqrt{3}$，2$\sqrt{2}$]

18．下列函数的单调区间：
（1）y=x-lnx
（2）y=ln（2x+3）+x²．

19．不等式ax+1＜0的解集为（$\frac{1}{3}$，+∞），则实数a=-3．

试题分类