题目内容
3.在△ABC中,已知b=$\frac{2\sqrt{3}}{3}$asinB,且cosB=cosC.则△ABC的形状为等腰三角形或等边三角形.分析 由条件利用正弦定理可得 3sinB=2$\sqrt{3}$sinAsinB,且B=C,化简可得sinA=$\frac{π}{3}$或$\frac{2π}{3}$,从而判断△ABC的形状.
解答 解:由题意,在△ABC中,2$\sqrt{3}$asinB=3b且cosB=cosC,
则有:3sinB=2$\sqrt{3}$sinAsinB,且B=C,B,C为锐角,
解得:sinA=$\frac{\sqrt{3}}{2}$,
∴A=$\frac{π}{3}$,或$\frac{2π}{3}$,
故:当A=$\frac{π}{3}$时,再由B=C可得△ABC是等边三角形.
当A=$\frac{2π}{3}$时,由B=C可得△ABC是等腰三角形.
故答案为:等腰三角形或等边三角形.
点评 本题主要考查正弦定理的应用,判断三角形的形状,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )
| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
11.设l,m,n是三条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
| A. | α∥β,l?α,n?β⇒l∥n | B. | l⊥n,l⊥α⇒n∥α | C. | l⊥α,l∥β⇒α⊥β | D. | α⊥β,l?α⇒l⊥β |
15.已知双曲线my2-x2=1(m∈R)与抛物线x2=8y有相同的焦点,则该双曲线的渐近线方程为( )
| A. | y=±$\sqrt{3}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
12.已知p:m∈(-2,-1),q:m满足$\frac{{x}^{2}}{2+m}-\frac{{y}^{2}}{m+1}=1$表示椭圆,那么p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
13.已知直线1经过点(0,1)且与直线2x-y+3=0平行,则直线1的方程为( )
| A. | x+2y-2=0 | B. | x-2y+2=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
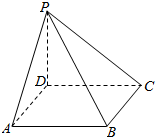 已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.