题目内容
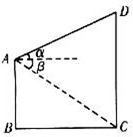如图，两座建筑物AB，CD的底部都在同一个水平面上，且AB、CD均与水平面垂直，它们的高度分别是9m和15m，从建筑物AB的顶部A看点D的仰角为α，看点C的俯角为β，已知α+β=45°，则BC的长度是考点：解三角形
专题：解三角形
分析：画出图形，结合图形，作AN⊥CD于N，利用直角三角形，结合两角和的正切值，求出BC的长度．
解答：
解：如图所示，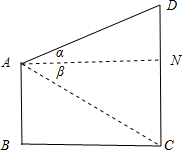
作AN⊥CD于N，
∵AB∥CD，AB=9，CD=15，
∴DN=6，NC=9；
设AN=x，则∠DAN=α，∠CAN=β，
且∠CAD=α+β=45°；
在Rt△ANC和Rt△AND中，
∵tanα=
，tanβ=
，
∴tan（α+β）=
=tan45°，
即
=1，
∴
+
-1=0，
整理，得x2-15x-54=0，
解得x1=18，x2=-3（舍去）；
∴BC的长度是18m．
故答案为：18．
作AN⊥CD于N，
∵AB∥CD，AB=9，CD=15，
∴DN=6，NC=9；
设AN=x，则∠DAN=α，∠CAN=β，
且∠CAD=α+β=45°；
在Rt△ANC和Rt△AND中，
∵tanα=
| 6 |
| x |
| 9 |
| x |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
即
| ||||
1-
|
∴
| 54 |
| x2 |
| 15 |
| x |
整理，得x2-15x-54=0，
解得x1=18，x2=-3（舍去）；
∴BC的长度是18m．
故答案为：18．
点评：本题考查了解三角形的应用问题，也考查了数学建模思想，方程思想以及两角和的正切公式的应用问题，是综合题．
练习册系列答案
相关题目