题目内容
5.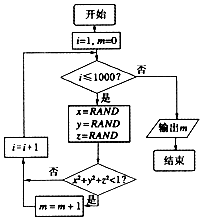 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )| A. | 3.126 | B. | 3.132 | C. | 3.151 | D. | 3.162 |
分析 我们可分析出程序的功能是利用随机模拟实验的方法求任取(0,1)上的x,y,z,求x2+y2+z2<1的概率,计算x2+y2+z2<1发生的概率为$\frac{π}{6}$,代入几何概型公式,即可得到答案.
解答 解:x2+y2+z2<1发生的概率为$\frac{4}{3}$π×13×$\frac{1}{8}$=$\frac{π}{6}$,
当输出结果为527时,i=1001,m=527,x2+y2+z2<1发生的概率为P=$\frac{527}{1000}$,
∴$\frac{527}{1000}$=$\frac{π}{6}$,
即π=3.162,
故选:D
点评 本题考查的知识点是程序框图,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键,本题属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.如图,某几何体的三视图都是直角三角形,若几何体的最大棱长为2,则该几何体的外接球的体积是( )
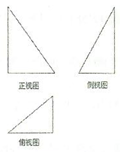

| A. | $\sqrt{6}π$ | B. | $\frac{4}{3}π$ | C. | 4π | D. | 6π |
13. 如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
 如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )| A. | A<4 | B. | A<5 | C. | A≤5 | D. | A≤6 |
20.设f(x)是定义在R上的奇函数,当x<0时,f(x)=2x+1,则f(0)+f(1)=( )
| A. | $-\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 5 |
10. 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
