题目内容
定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(-2,-1)∪[3,5)的长度d=[(-1)-(-2)]+(5-3)=3.用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]•{x},g(x)=x-1,当0≤x≤5时,则不等式f(x)<g(x)的解集区间的长度为( )
| A、1 | B、2 | C、3 | D、4 |
考点:其他不等式的解法
专题:计算题,函数的性质及应用
分析:依题意,对x分0≤x<1与1≤x≤5讨论,利用作差法,放缩法即可求得当0≤x≤5时,不等式f(x)<g(x)的解集区间的长度.
解答:
解:当0≤x<1时,[x]=0,f(x)=0,g(x)<0,
∴f(x)>g(x);
当1≤x≤5时,若n≤x<n+1(1≤n≤4),则[x]=n;
∴f(x)-g(x)=n(x-n)-x+1=x(n-1)-n2+1<(n+1)(n-1)-n2+1=0,
即f(x)<g(x);
∴不等式f(x)<g(x)的解集区间的长度为4-1=3.
故选:C.
∴f(x)>g(x);
当1≤x≤5时,若n≤x<n+1(1≤n≤4),则[x]=n;
∴f(x)-g(x)=n(x-n)-x+1=x(n-1)-n2+1<(n+1)(n-1)-n2+1=0,
即f(x)<g(x);
∴不等式f(x)<g(x)的解集区间的长度为4-1=3.
故选:C.
点评:本题考查抽象不等式的解法,考查作差法与放缩法的综合应用,考查理解与转化解决问题的能力,属于难题.

练习册系列答案
相关题目
为了调查城市PM2.5的情况,按地域把48个城市分成大型、中型、小型三组,对应的城市数分别为8,16,24.若用分层抽样的方法抽取12个城市,则中型组中应抽取的城市数为( )
| A、3 | B、4 | C、5 | D、6 |
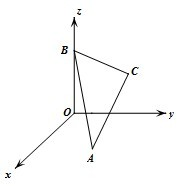 如图,空间直角坐标系Oxyz中,正三角形ABC的顶点A,B分别在xOy平面和z轴上移动.若AB=2,则点C到原点O的最远距离为( )
如图,空间直角坐标系Oxyz中,正三角形ABC的顶点A,B分别在xOy平面和z轴上移动.若AB=2,则点C到原点O的最远距离为( )A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
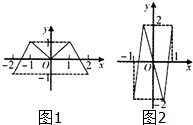 如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )
如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )| A、18 | B、21 | C、24 | D、27 |
关于直线l、m与平面α、β的命题中,一定正确的是( )
| A、若l∥m,m?α,则l∥α |
| B、若l⊥β,α⊥β,则l∥α |
| C、若l?β,α⊥β,则l⊥α |
| D、若l⊥β,α∥β,则l⊥α |
直线l:y=k(x-2)+2与圆C:x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是( )
| A、(一∞,一1) |
| B、(一1,1) |
| C、(一1,+∞) |
| D、(一∞,一1)∪(一1,+∞) |