题目内容
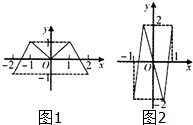如图，偶函数f（x）的图象形如字母M（图1），奇函数g（x）的图象形如字母N（图2），若方程f（g（x））=0．g（f（x））=0的实根个数分别为a，b，则a+b=（ ）| A、18 | B、21 | C、24 | D、27 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：结合函数图象把方程根的个数转化为函数图象的交点个数，可分别求得a，b进而可得答案．
解答：
解：由图象知，f（x）=0有3个根，0，±
，
g（x）=0有3个根，0，±
（假设与x轴交点横坐标为±
），
由f（g（x））=0，得g（x）=0或±
，
由图象可知g（x）所对每一个值都能有3个根，因而a=9；
由g（f（x））=0，知f（x）=0 或±
，
由图象可可以看出0时对应有3个根，
而
时有4个，
而-
时只有2个，加在一起也是9个，
即b=9，
∴a+b=9+9=18，
故选：A．
| 3 |
| 2 |
g（x）=0有3个根，0，±
| 3 |
| 4 |
| 3 |
| 4 |
由f（g（x））=0，得g（x）=0或±
| 3 |
| 2 |
由图象可知g（x）所对每一个值都能有3个根，因而a=9；
由g（f（x））=0，知f（x）=0 或±
| 3 |
| 4 |
由图象可可以看出0时对应有3个根，
而
| 3 |
| 4 |
而-
| 3 |
| 4 |
即b=9，
∴a+b=9+9=18，
故选：A．
点评：本题主要考查函数函数的图象及其应用，考查方程根的个数，利用数形结合思想是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知全集U=R，集合A={1，2，3，4，5}，B=[3，+∞），则图中阴影部分所表示的集合为（ ）
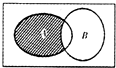
| A、{0，1，2} |
| B、{0，1} |
| C、{1，2} |
| D、{1} |
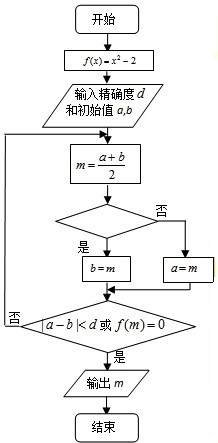如图是用二分法求方程f（x）=0近似解的程序框图，其中f（a）f（b）＜0．判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0；
②f（a）f（m）＞0；
③f（b）f（m）＜0；
④f（b）f（m）＞0．
其中正确的是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
函数f(x)=sin(ωx+φ)(ω＞0，|φ|＜
)的最小正周期为π，若其图象向右平移
个单位后关于y轴对称，则（ ）
| π |
| 2 |
| π |
| 3 |
A、ω=2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=4，φ=
| ||
D、ω=2，φ=-
|
集合A={-1，0，1}，B={y|y=x2+1，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{0，1} | D、{-1，0，1} |
已知函数g（x）是偶函数，f（x）=g（x-2），且当x≠2时其导函数f（x）满足（x-2）f′（x）＞0，若1＜a＜3，则（ ）
| A、f（4a）＜f（3）＜f（log3a） |
| B、f（3）＜f（log3a）＜f（4a） |
| C、f（log3a）＜f（3）＜f（4a） |
| D、f（log3a）＜f（4a）＜f（3） |