题目内容
已知sinxcosy=
,则cosxsiny的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1,1] |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由题意可得-1≤sin(x+y)≤1,sin(x+y)=
+cosxsiny,由此求得cosxsiny的取值范围.再根据
-cosxsiny=sin(x-y ),且-1≤sin (x-y )≤1,求得cosxsiny的范围,再把这两个范围取交集,即得所求.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由于-1≤sin(x+y)≤1,sinxcosy=
,
sin(x+y)=sinxcosy+cosxsiny=
+cosxsiny,
故有-
≤cosxsiny≤
①.
再根据 sinxcosy-cosxsiny=sin(x-y ),且-1≤sin (x-y )≤1,
∴-1≤
-cosxsiny≤1,∴-
≤cosxsiny≤
②.
结合①②可得-
≤cosxsiny≤
故选:A.
| 1 |
| 2 |
sin(x+y)=sinxcosy+cosxsiny=
| 1 |
| 2 |
故有-
| 3 |
| 2 |
| 1 |
| 2 |
再根据 sinxcosy-cosxsiny=sin(x-y ),且-1≤sin (x-y )≤1,
∴-1≤
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
结合①②可得-
| 1 |
| 2 |
| 1 |
| 2 |
故选:A.
点评:本题主要考查两角和的正弦公式,正弦函数的值域,属于中档题.

练习册系列答案
相关题目
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
如图,在△ABC中,AB=1,AC=3,D是BC的中点,则
•
=( )
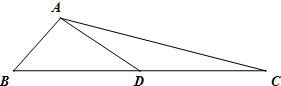
| AD |
| DC |

| A、3 | B、2 | C、5 | D、不确定 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
把1100(2)化为十进制数,则此数为( )
| A、8 | B、12 | C、16 | D、20 |
如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知x,y之间的数据如下表所示,则y与x之间的线性回归方程必过点( )
| x | 1.08 | 1.12 | 1.19 | 1.30 |
| y | 2.25 | 2.37 | 2.40 | 2.60 |
| A、(0,0) |
| B、(1.17,0) |
| C、(0,2.41) |
| D、(1.17,2.41) |