题目内容
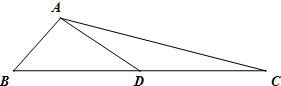
如图，在△ABC中，AB=1，AC=3，D是BC的中点，则
•
=（ ）
| AD |
| DC |
| A、3 | B、2 | C、5 | D、不确定 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：根据平面向量的平行四边形法则及减法三角形法则可得，
•
=
(
+
)•
=
(
+
)•
(
-
)=
(
2-
2)，结合已知条件可得答案．
| AD |
| DC |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 4 |
| AC |
| AB |
解答：
解：∵D是BC的中点，
∴
•
=
(
+
)•
=
(
+
)•
(
-
)
=
(
2-
2)=
(32-12)=2，
故选：B．
∴
| AD |
| DC |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| BC |
=
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AC |
| AB |
=
| 1 |
| 4 |
| AC |
| AB |
| 1 |
| 4 |
故选：B．
点评：本题考查平面向量的数量积运算、平行四边形法则、三角形法则，属基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
已知函数f（x）=sin（ωx+
）（ω＞0），若存在实数x0使得对任意的实数x，都有f（x0）≤f（x）≤f（x0+2013）成立，则ω的最小值是（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|（x-1）（x-4）＞0}，B={x|log2x＜1}，则集合（∁RA）∩B=（ ）
| A、{x|1≤x≤4} |
| B、{x|0＜x＜2} |
| C、{x|1≤x＜2} |
| D、{x|2＜x≤4} |
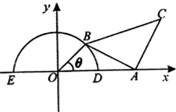如图，半圆的圆心在直角坐标原点，点A，D，E的坐标分别为A（2，0），D（1，0），E（-1，0），且点B在半圆上自点D逆时针向点E运动，三角形ABC是等腰直角三形，∠BAC是直角，则四边形OACB的面积的最大值是（ ）A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
下列命题正确的是（ ）
A、若
| ||||||||
B、若
| ||||||||
C、向量
| ||||||||
| D、两向量相等的充要条件是它们的始点、终点相同 |
已知sinxcosy=
，则cosxsiny的取值范围是（ ）
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1，1] |
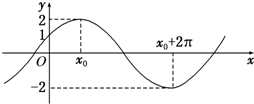如图，已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜