题目内容
已知0<a<b,m>0,求证:
>
.
| a+m |
| b+m |
| a |
| b |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:利用作差法,结合条件,即可证明结论.
解答:
证明:
-
=
=
∵0<a<b,∴b-a>0,
又m>0,∴b(b+m)>0
∴
>0,
∴
-
>0,即
>
.
| a+m |
| b+m |
| a |
| b |
| ab+bm-ab-am |
| b(b+m) |
| m(b-a) |
| b(b+m) |
∵0<a<b,∴b-a>0,
又m>0,∴b(b+m)>0
∴
| m(b-a) |
| b(b+m) |
∴
| a+m |
| b+m |
| a |
| b |
| a+m |
| b+m |
| a |
| b |
点评:本题考查不等式的证明,考查作差法的运用,比较基础.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
数23有可能是数列3,5,7,9,11,…中的第( )项.
| A、10 | B、11 | C、12 | D、13 |
在平行四边形ABCD中,若|
|2-|
|2=2|
|•|
|,则∠BAD=( )
| AC |
| BD |
| AB |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
若变量x,y满足线性约束条件
,且3x+y的最小值为1,则a=( )
|
| A、0 | B、-1 | C、1 | D、2 |
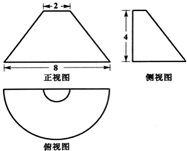 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于