题目内容
已知函数f(x)=2cosxsin(x+
)-
sin2x+sinxcosx.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,
]上的最值和单调递增区间;
(3)f(x)的图象可以由y=sin2x图象经过怎样变换所得.
| π |
| 3 |
| 3 |
(1)求f(x)的最小正周期;
(2)求f(x)在[0,
| π |
| 3 |
(3)f(x)的图象可以由y=sin2x图象经过怎样变换所得.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)将函数进行化简,根据三角函数的周期公式即可求函数f(x)的最小正周期T;
(2)由三角函数的单调性即可求函数f(x)的单调递增区间;
(3)根据三角函数的单调性即可求函数f(x)在区间[0,
]上的值域.
(2)由三角函数的单调性即可求函数f(x)的单调递增区间;
(3)根据三角函数的单调性即可求函数f(x)在区间[0,
| π |
| 3 |
解答:
解:f(x)=2cosxsin(x+
)-
sin2x+sinxcosx
=2cosx(
sinx+
cosx)-
sin2x+sinxcosx
=2sinxcosx+
(cos2x-sin2x)
=sin2x+
cos2x=2sin(2x+
),
(1)则函数f(x)的最小正周期T=
=π;
(2)若x∈[0,
],则2x+
∈[
,π],
则当2x+
=
时,函数f(x)取得最大值f(x)=2,
当2x+
=π,函数f(x)取得最小值f(x)=2×sinπ=0,
即函数f(x)在区间[0,
]上的值域[0,2].
由-
+2kπ≤2x+
≤
+2kπ,解得-
+kπ≤x≤kπ+
,k∈Z,
即函数f(x)的单调递增区间[-
+kπ,kπ+
],k∈Z;
(3)f(x)的图象可以由y=sin2x图象经过向左平移
,然后横坐标不变,纵坐标伸长为原来的2倍得到.
| π |
| 3 |
| 3 |
=2cosx(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=2sinxcosx+
| 3 |
=sin2x+
| 3 |
| π |
| 3 |
(1)则函数f(x)的最小正周期T=
| 2π |
| 2 |
(2)若x∈[0,
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
则当2x+
| π |
| 3 |
| π |
| 2 |
当2x+
| π |
| 3 |
即函数f(x)在区间[0,
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
即函数f(x)的单调递增区间[-
| 5π |
| 12 |
| π |
| 12 |
(3)f(x)的图象可以由y=sin2x图象经过向左平移
| π |
| 6 |
点评:本题主要考查三角函数函数的周期和单调区间和值域的求解,关键在正确化简三角函数解析式为一个角的一个三角函数名称的形式,然后利用三角函数的性质解答;要求熟练掌握三角函数的图象和性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(1,2),
=(2,3),则λ<-4是向量
=λ
+
与向量
=(3,-1)夹角钝角的( )
| a |
| b |
| m |
| a |
| b |
| n |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
已知集合M={5,6,7},N={5,7,8},则( )
| A、M⊆N |
| B、M?N |
| C、M∩N={5,7} |
| D、M∪N={6,7,8} |
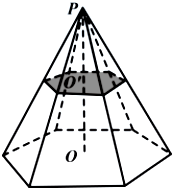 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.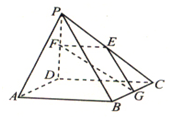 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.