题目内容
在极坐标系中,设曲线C1:ρ=2sinθ,C2:ρ=2cosθ分别相较于A、B两点,则线段AB直平分线的极坐标方程为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把曲线的极坐标分别化为直角坐标方程联立可得交点坐标,求出线段AB的垂直平分线的方程,再化为直角坐标方程即可.
解答:
解:曲线C1:ρ=2sinθ,化为ρ2=2ρsinθ,∴x2+y2=2y.
C2:ρ=2cosθ化为ρ2=2ρcosθ,∴x2+y2=2x.
联立
,解得
,
.
∴A(0,0),B(1,1).
线段AB的中点为M(
,
).
∵kAB=1,∴线段AB直平分线的斜率k=-1.
∴线段AB直平分线的直角坐标方程为:y-
=-(x-
),
化为x+y=1.
∴线段AB直平分线的极坐标方程为ρcosθ+ρsinθ=1.
故答案为:ρcosθ+ρsinθ=1.
C2:ρ=2cosθ化为ρ2=2ρcosθ,∴x2+y2=2x.
联立
|
|
|
∴A(0,0),B(1,1).
线段AB的中点为M(
| 1 |
| 2 |
| 1 |
| 2 |
∵kAB=1,∴线段AB直平分线的斜率k=-1.
∴线段AB直平分线的直角坐标方程为:y-
| 1 |
| 2 |
| 1 |
| 2 |
化为x+y=1.
∴线段AB直平分线的极坐标方程为ρcosθ+ρsinθ=1.
故答案为:ρcosθ+ρsinθ=1.
点评:本题考查了曲线的极坐标与直角坐标方程的互化、线段的垂直平分线的方程的求法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
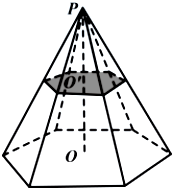 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.