题目内容
已知sinx+cosx=
,且0<x<π.
(1)求sinx、cosx、tanx的值;
(2)求sin3x-cos3x的值.
| 1 |
| 5 |
(1)求sinx、cosx、tanx的值;
(2)求sin3x-cos3x的值.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)先根据sinx+cosx的值和二者的平方关系联立求得cosx的值,进而根据同角三角函数的基本关系求得sinx的值,最后利用商数关系求得tanx的值.
(2)利用(1)的结论,即可求出.
(2)利用(1)的结论,即可求出.
解答:
解:(1)由sinx+cosx=
,得sinx=
-cosx,代入sin2x+cos2x=1得:(5cosx-4)(5cosx+3)=0,
∴cosx=
或cosx=-
,当cosx=
时,得sinx=-
,又∵0<x<π,
∴sinx>0,故这组解舍去;
当cosx=-
时,sinx=
,tanx=-
.
(2)由(1)得sin3x-cos3x=(
)3-(-
)3=
.
| 1 |
| 5 |
| 1 |
| 5 |
∴cosx=
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴sinx>0,故这组解舍去;
当cosx=-
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
(2)由(1)得sin3x-cos3x=(
| 4 |
| 5 |
| 3 |
| 5 |
| 91 |
| 125 |
点评:本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的正负号.

练习册系列答案
相关题目
函数y=2|X-1|的图象为( )
A、 |
B、 |
C、 |
D、 |
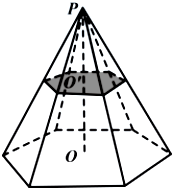 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′. 如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.
如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.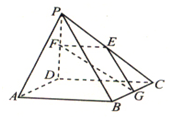 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.