题目内容
将二进制数101 1（2） 化为十进制数，结果为 ；将十进制数124转化为八进制数，结果为 ．
考点：进位制
专题：计算题
分析：根据二进制转化为十进制的方法，我们分别用每位数字乘以权重，累加后即可得到结果；利用“除k取余法”是将十进制数除以8，然后将商继续除以8，直到商为0，然后将依次所得的余数倒序排列即可得到答案．
解答：
解：1011（2）=1×20+1×21+0×22+1×23
=1+2+8
=11．
124÷8=15…4，
15÷8=1…7，
1÷8=0…1，
∴1 011001（2）=174（8）
故答案为：11，174（8）
=1+2+8
=11．
124÷8=15…4，
15÷8=1…7，
1÷8=0…1，
∴1 011001（2）=174（8）
故答案为：11，174（8）
点评：本题考查的知识点是不同进制数之间的转换，解答的关键是熟练掌握不同进制之间数的转化规则．
练习册系列答案
相关题目
函数y=2|X-1|的图象为（ ）
A、 |
B、 |
C、 |
D、 |
已知向量
=（1，2），
=（2，3），则λ＜-4是向量
=λ
+
与向量
=（3，-1）夹角钝角的（ ）
| a |
| b |
| m |
| a |
| b |
| n |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
已知集合M={5，6，7}，N={5，7，8}，则（ ）
| A、M⊆N |
| B、M?N |
| C、M∩N={5，7} |
| D、M∪N={6，7，8} |
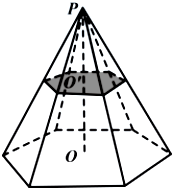如图，正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截，得到正六棱台OO′和较小的棱锥PO′．