题目内容
记
ai=a1+a2+a3+…+an,则函数f(x)=
|x-n|的最小值为 .
| n |
 |
| i=1 |
| 21 |
 |
| n=1 |
考点:数列的求和
专题:函数的性质及应用,等差数列与等比数列
分析:由绝对值的不等式结合等差数列的前n项和得到函数f(x)=
|x-n|的最小值=
(n2-1),取n=21得答案.
| n |
 |
| i=1 |
| 1 |
| 4 |
解答:
解:由|x-1|+|x-n|≥丨n-x+x-1丨=n-1,
同理:
|x-2|+|x-(n-1)|≥n-3,
|x-3|+|x-(n-2)|≥n-5,
…
|x-
(n-1)|+|x-
(n+3)|≥2,
当x=
(n+1)(即1,n的中点)有|x-
(n+1)|取最小值0.
故函数f(x)=
|x-n|的最小值=0+2+4+…+(n-3)+(n-1)=
(n2-1),
此时x=
(n+1).
∴当x=
(21+1)=11时,函数f(x)=
|x-n|的最小值为
×(212-1)=110.
故答案为:110.
同理:
|x-2|+|x-(n-1)|≥n-3,
|x-3|+|x-(n-2)|≥n-5,
…
|x-
| 1 |
| 2 |
| 1 |
| 2 |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
故函数f(x)=
| n |
 |
| i=1 |
| 1 |
| 4 |
此时x=
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 21 |
 |
| n=1 |
| 1 |
| 4 |
故答案为:110.
点评:本题考查了数列的函数特性,考查了等差数列的前n项和,训练了绝对值不等式的用法,是中档题.

练习册系列答案
相关题目
已知集合M={5,6,7},N={5,7,8},则( )
| A、M⊆N |
| B、M?N |
| C、M∩N={5,7} |
| D、M∪N={6,7,8} |
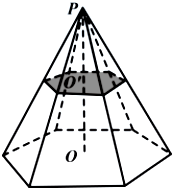 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′. 如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.
如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.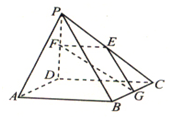 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.