题目内容
已知数列{an}的前n项和Sn满足Sn=1+10n-n2.
(1)求{an}的通项公式;
(2)求Sn最大值和对应的n值.
(1)求{an}的通项公式;
(2)求Sn最大值和对应的n值.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用an=
,能求出{an}的通项公式.
(2)由Sn=1+10n-n2,利用配方法能求出Sn最大值和对应的n值.
|
(2)由Sn=1+10n-n2,利用配方法能求出Sn最大值和对应的n值.
解答:
解:(1)∵Sn=1+10n-n2,
∴a1=S1=1+10-12=10,
n≥2时,an=Sn-Sn-1=(1+10n-n2)-[1+10(n-1)-(n-1)2]=11-2n,
n=1时,11-2n=9≠a1,
∴an=
.
(2)∵Sn=1+10n-n2=-(n-5)2+26,
∴当n=5时,Sn取最大值26.
∴a1=S1=1+10-12=10,
n≥2时,an=Sn-Sn-1=(1+10n-n2)-[1+10(n-1)-(n-1)2]=11-2n,
n=1时,11-2n=9≠a1,
∴an=
|
(2)∵Sn=1+10n-n2=-(n-5)2+26,
∴当n=5时,Sn取最大值26.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的最大值的求法,解题时要注意配方法的合理运用.

练习册系列答案
相关题目
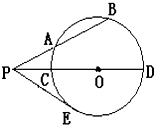 如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7
如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7