题目内容
已知f(x)=
,g(x)=ax+5-2a(a>0),f(x)的值域为A,g(x)的值域为B.若?x1∈[0,1],?x2∈[0,1],f(x1)=g(x2),则a的范围是 .
| 2x2 |
| x+1 |
考点:函数的值
专题:计算题,函数的性质及应用
分析:由题意化简f(x)=
=
=2(x+1)+
-4,从而求得0≤f(x)≤1,则原题可化为?x2∈[0,1],使0≤g(x2)≤1,从而求a的范围.
| 2x2 |
| x+1 |
| 2(x+1)2-4(x+1)+2 |
| x+1 |
| 2 |
| x+1 |
解答:
解:由题意,
f(x)=
=
=2(x+1)+
-4,
∵x+1∈[1,2],
∴4≤2(x+1)+
≤5,
则0≤f(x)≤1,
则原题可化为?x2∈[0,1],使0≤g(x2)≤1,
又∵g(x)=ax+5-2a(a>0)在[0,1]上是增函数,
∴0≤g(0)=5-2a≤1或0≤g(1)=5-a≤1,
解得,2≤a≤
或4≤a≤5.
故答案为:2≤a≤
或4≤a≤5.
f(x)=
| 2x2 |
| x+1 |
| 2(x+1)2-4(x+1)+2 |
| x+1 |
=2(x+1)+
| 2 |
| x+1 |
∵x+1∈[1,2],
∴4≤2(x+1)+
| 2 |
| x+1 |
则0≤f(x)≤1,
则原题可化为?x2∈[0,1],使0≤g(x2)≤1,
又∵g(x)=ax+5-2a(a>0)在[0,1]上是增函数,
∴0≤g(0)=5-2a≤1或0≤g(1)=5-a≤1,
解得,2≤a≤
| 5 |
| 2 |
故答案为:2≤a≤
| 5 |
| 2 |
点评:本题考查了函数的化简与函数的值域的求法,同时考查了存在性问题的处理方法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=[ax2+(a-1)2x+a-(a-1)2]ex(其中a∈R).
(1)若x=0为f(x)的极值点,求a得值;
(2)在(1)的条件下,解不等式f(x)>(x-1)(
x2+x+1).
(1)若x=0为f(x)的极值点,求a得值;
(2)在(1)的条件下,解不等式f(x)>(x-1)(
| 1 |
| 2 |
若将函数y=sin(ωx+
)(ω>0)的图象向左平移
个单位,与函数y=sin(ωx+
)的图象重合,则ω的最小值为( )
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
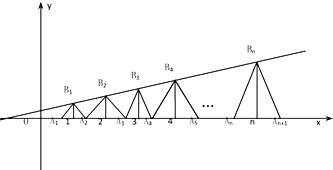 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=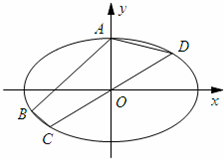 已知椭圆G:
已知椭圆G: