题目内容
已知关于x的方程32x+1+(m-1)(3x+1-1)-(m-3)3x=0有两个不同的实数解,则m的取值范围是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:令3x=t,得到f(x)=32x+1+(m-1)(3x+1-1)-(m-3)•3x=3t2+2mt-m+1.设y=3t2+2mt-m+1,结合二次函数的性质从而得到答案.
解答:
解:令3x=t,f(x)=32x+1+(m-1)(3x+1-1)-(m-3)•3x=3t2+2mt-m+1.
设y=3t2+2mt-m+1.由题设知该方程有两个根0<t1<t2,
∴
,
解得m<-
.
故答案为:(-∞,-
).
设y=3t2+2mt-m+1.由题设知该方程有两个根0<t1<t2,
∴
|
解得m<-
3+
| ||
| 2 |
故答案为:(-∞,-
3+
| ||
| 2 |
点评:本题考查了二次函数的性质,考查了转化思想,是一道中档题.

练习册系列答案
相关题目
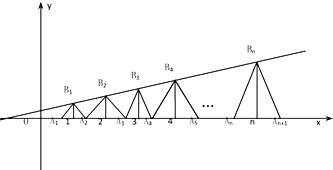 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=