题目内容
已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是指数函数,且f(2)=
.
(1)当x>0时,求f(x)的表达式;
(2)当x≤0时,求f(x)的表达式;
(3)画y=f(x),x∈[-4,0]的图象,并指出函数的值域.
| 1 |
| 4 |
(1)当x>0时,求f(x)的表达式;
(2)当x≤0时,求f(x)的表达式;
(3)画y=f(x),x∈[-4,0]的图象,并指出函数的值域.
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)求解即可得到y=ax,a2=
,a=
,(2)当x=0时,f(0)=0,当x<0时,-x>0,转化为当x>0时,f(x)=(
)x求解.(3)画出图象,利用图象求解.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:(1)∵当x>0时,f(x)的表达式是指数函数,且f(2)=
解:(1)∵当x>0时,f(x)的表达式是指数函数,且f(2)=
.
∴y=ax,a2=
,a=
,
当x>0时,f(x)=(
)x;
(2)∵定义在R上的奇函数f(x),
∴f(-x)=-f(x),
当x=0时,f(0)=0,
当x<0时,-x>0,
∴f(x)=-f(-x)=-(
)-x=-2x
∴当x≤0时,f(x)=
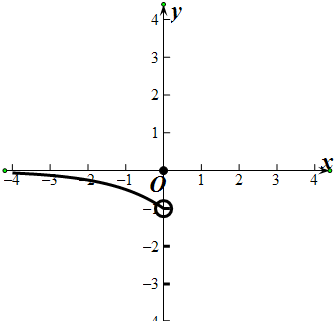
(3)y=f(x),x∈[-4,0]的图象
值域为:(-1,-
]∪{0}
 解:(1)∵当x>0时,f(x)的表达式是指数函数,且f(2)=
解:(1)∵当x>0时,f(x)的表达式是指数函数,且f(2)=| 1 |
| 4 |
∴y=ax,a2=
| 1 |
| 4 |
| 1 |
| 2 |
当x>0时,f(x)=(
| 1 |
| 2 |
(2)∵定义在R上的奇函数f(x),
∴f(-x)=-f(x),
当x=0时,f(0)=0,
当x<0时,-x>0,
∴f(x)=-f(-x)=-(
| 1 |
| 2 |
∴当x≤0时,f(x)=
|
(3)y=f(x),x∈[-4,0]的图象
值域为:(-1,-
| 1 |
| 16 |
点评:本题考查了函数的概念,性质,属于中档题,有点难度.

练习册系列答案
相关题目
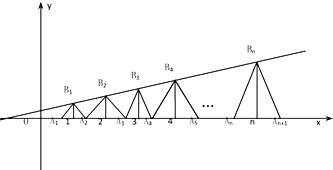 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=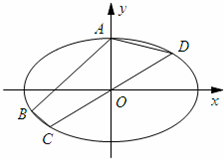 已知椭圆G:
已知椭圆G: