题目内容
已知向量
=(mx2,-1),
=(
,x)(m是常数),且f(x)=
.
(1)若f(x)是奇函数,求m的值;
(2)设函数g(x)=f(
)-
,讨论当实数m变化时,函数g(x)零点的个数.
| a |
| b |
| 1 |
| mx-1 |
| 1 | ||||
|
(1)若f(x)是奇函数,求m的值;
(2)设函数g(x)=f(
| x |
| 2 |
| x |
| 2 |
考点:平面向量数量积的运算,函数奇偶性的性质
专题:函数的性质及应用,平面向量及应用
分析:(1)首先把给出的两个向量的坐标代入函数解析式,化简后运用奇函数的定义即可求解使函数f(x)为奇函数的实数m的值;
(2)g(x)=f(
)-
=m-
-
=
,令h(x)=-x2+2mx-4,利用判别式判断二次函数零点的情况,即可得出结论.
(2)g(x)=f(
| x |
| 2 |
| x |
| 2 |
| 2 |
| x |
| x |
| 2 |
| -x2+2mx-4 |
| 2x |
解答:
解:(1)由题意知
•
=
-x=
,
所以f(x)=
=
=m-
.
由题知对任意的不为零的实数x,都有f(-x)=-f(x),
即m+
=-m+
成立,所以m=0.
(2)g(x)=f(
)-
=m-
-
=
,
令h(x)=-x2+2mx-4,∴△=4m2-16,则有△>0得,m<-4或m>4时,h(x)有两个零点,
由△=0得,m=±4时,h(x)有一个零点,
由△<0得,-4<m<4时,h(x)没有零点,
∴m<-4或m>4时,g(x)有两个零点,m=±4时,g(x)有一个零点,-4<m<4时,g(x)没有零点,
| a |
| b |
| mx2 |
| mx-1 |
| x |
| mx-1 |
所以f(x)=
| 1 | ||||
|
| mx-1 |
| x |
| 1 |
| x |
由题知对任意的不为零的实数x,都有f(-x)=-f(x),
即m+
| 1 |
| x |
| 1 |
| x |
(2)g(x)=f(
| x |
| 2 |
| x |
| 2 |
| 2 |
| x |
| x |
| 2 |
| -x2+2mx-4 |
| 2x |
令h(x)=-x2+2mx-4,∴△=4m2-16,则有△>0得,m<-4或m>4时,h(x)有两个零点,
由△=0得,m=±4时,h(x)有一个零点,
由△<0得,-4<m<4时,h(x)没有零点,
∴m<-4或m>4时,g(x)有两个零点,m=±4时,g(x)有一个零点,-4<m<4时,g(x)没有零点,
点评:本题考查了平面向量数量积的坐标表示,模、夹角,考查了函数的奇偶性,考查了分类讨论的数学思想及数学转化思想,解答此题的关键是正确写出两个向量的数量积.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知函数f(x)=[ax2+(a-1)2x+a-(a-1)2]ex(其中a∈R).
(1)若x=0为f(x)的极值点,求a得值;
(2)在(1)的条件下,解不等式f(x)>(x-1)(
x2+x+1).
(1)若x=0为f(x)的极值点,求a得值;
(2)在(1)的条件下,解不等式f(x)>(x-1)(
| 1 |
| 2 |
若将函数y=sin(ωx+
)(ω>0)的图象向左平移
个单位,与函数y=sin(ωx+
)的图象重合,则ω的最小值为( )
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
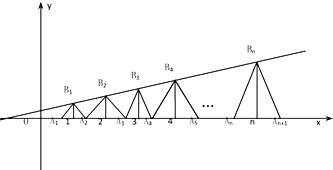 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=