题目内容
已知函数f(x)存在反函数f-1(x),且f(x)+f(-x)=2,则f-1(x-2)+f-1(4-x)等于( )
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
考点:反函数
专题:解题思想
分析:函数的定义域是反函数的值域,函数的值域是反函数的定义域,函数与反函数的对应关系正好相反.
解答:
解:∵f(x)+f(-x)=2,
对函数 f(x)而言,自变量之和等于0时,函数值之和等于2,
∴对反函数 f-1(x)而言,自变量之和等于2时,函数值之和等于0,
又∵x-2+4-x=2,
∴f-1(x-2)+f-1(4-x)=0,
故选B.
对函数 f(x)而言,自变量之和等于0时,函数值之和等于2,
∴对反函数 f-1(x)而言,自变量之和等于2时,函数值之和等于0,
又∵x-2+4-x=2,
∴f-1(x-2)+f-1(4-x)=0,
故选B.
点评:本题考查反函数的概念,函数与反函数的定义域、值域、对应法则间的关系.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 .对
.对 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项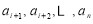 的最小值记为
的最小值记为 ,
, .
. 为
为 ,写出
,写出 ,
, ,
, 的值;
的值; (
( )是公比大于
)是公比大于 的等比数列,且
的等比数列,且 .证明:
.证明: 是等比数列;
是等比数列; 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列. ,其中
,其中 ,且
,且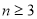 ,若对
,若对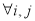 (
(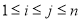 ),
),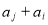 与
与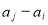 两数中至少有一个属于
两数中至少有一个属于 ,则称数集
,则称数集 具有性质
具有性质
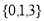 与数集
与数集 是否具有性质
是否具有性质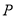 ,说明理由
,说明理由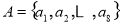 具有性质
具有性质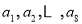 是否为等差数列,若是等差数列,请证明;若不是,请说明理由
是否为等差数列,若是等差数列,请证明;若不是,请说明理由