题目内容
已知椭圆C:
+
=1,直线l:(2m+1)x+(1-m)y-5m-4=0(m∈R)
(1)证明:不论m取任何实数,直线l与椭圆C恒交于两点;
(2)设直线l与椭圆C的两个交点为A.B,M为弦AB的中点,O为坐标原点,当m∈R且m≠-
,m≠1时,记直线l的斜率为kAB,直线OM的斜率为kOM,求证:kABkOM为定值.
| x2 |
| 16 |
| y2 |
| 9 |
(1)证明:不论m取任何实数,直线l与椭圆C恒交于两点;
(2)设直线l与椭圆C的两个交点为A.B,M为弦AB的中点,O为坐标原点,当m∈R且m≠-
| 1 |
| 2 |
考点:圆锥曲线的综合
专题:常规题型,综合题
分析:(1)直线l:(2m+1)x+(1-m)y-5m-4=0(m∈R)必过点(3,1),而此点(3,1)在椭圆C内,即可得出不论m取任何实数,直线l与椭圆C恒交于两点;
(2)设出A,B两点的坐标求出中点M的坐标,根据题意表示出kABkOM=
,再利用点在椭圆上点的坐标适合椭圆方程代入可得答案.
(2)设出A,B两点的坐标求出中点M的坐标,根据题意表示出kABkOM=
| ||||
|
解答:
解:(1)∵直线l:(2m+1)x+(1-m)y-5m-4=0(m∈R)可化为:
m(2x-y-5)+(x+y-4)=0,
由
得:
故直线必过点(3,1),而此点(3,1)在椭圆C内,
∴不论m取任何实数,直线l与椭圆C恒交于两点;
(2)由题意得:设A(x1,y1)B(x2,y2),则中点M(
,
),
所以kAB=
,kOM=
,
所以kAB•kOM=
,
又因为点A(x1,y1)B(x2,y2)在椭圆上
所以9x12+16y12=144,9x22+16y22=144,
所以得9(x22-x12)+16(y22-y12)=0,
所以
=-
.
故kABkOM为定值-
.
m(2x-y-5)+(x+y-4)=0,
由
|
|
故直线必过点(3,1),而此点(3,1)在椭圆C内,
∴不论m取任何实数,直线l与椭圆C恒交于两点;
(2)由题意得:设A(x1,y1)B(x2,y2),则中点M(
| x1+ x2 |
| 2 |
| y1+ y2 |
| 2 |
所以kAB=
| y2- y1 |
| x2-x1 |
| y2+ y1 |
| x2+x1 |
所以kAB•kOM=
| ||||
|
又因为点A(x1,y1)B(x2,y2)在椭圆上
所以9x12+16y12=144,9x22+16y22=144,
所以得9(x22-x12)+16(y22-y12)=0,
所以
| ||||
|
| 9 |
| 16 |
故kABkOM为定值-
| 9 |
| 16 |
点评:解决此类题目的关键是利用设而不求的方法,即设出点的坐标而不求点的坐标直接根据题意写出表达式进行整体求解,此种方法在圆锥曲线部分常见.

练习册系列答案
相关题目
设f(x)是定义域为R的奇函数,且在(0,+∞)上是减函数,若f(1)=0,则不等式f(x)>0的解集是( )
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
空间四个不同的平面,它们有多种位置关系,从交线数目看,所有可能出现的交线数目的集合是( )
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
已知函数f(x)存在反函数f-1(x),且f(x)+f(-x)=2,则f-1(x-2)+f-1(4-x)等于( )
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
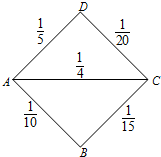 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为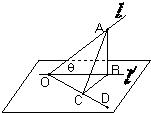 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.