题目内容
设甲，乙两名射手各打10发子弹，每发子弹击中环数如下：
甲：10，6，7，10，8，9，9，10，5，10；
乙：8，7，9，10，9，8，7，9，8，9．
试问哪一名射手的技术较好？
甲：10，6，7，10，8，9，9，10，5，10；
乙：8，7，9，10，9，8，7，9，8，9．
试问哪一名射手的技术较好？
考点：极差、方差与标准差
专题：计算题
分析：先做出两组数据的平均数，发现平均数相等，从平均数上不能区分两组数据的好坏，又求两组数据的方差，从稳定程度上来比较两个人的技术好坏，得到乙的水平较高．
解答：
解：先计算两名射手的平均环数：
=
(10+6+7+10+8+9+9+10+5+10)=8.4
=
(8+7+9+10+9+8+7+9+8+9)=8.4
再计算两名射手的标准差：
s甲=
=
s乙=
=
∴两名射手的平均值相等，但是乙的稳定性要好，
∴乙的水平比甲好．
. |
| x甲 |
| 1 |
| 10 |
. |
| x乙 |
| 1 |
| 10 |
再计算两名射手的标准差：
s甲=
|
| 1.884 |
s乙=
|
| 0.854 |
∴两名射手的平均值相等，但是乙的稳定性要好，
∴乙的水平比甲好．
点评：本题考查两组数据的平均数和方差，来判断两个人的射击水平好坏，本题是一个统计部分经常出现的一个问题，本题由于数据运算比较困难，是一个易错题．
练习册系列答案
相关题目
空间四个不同的平面，它们有多种位置关系，从交线数目看，所有可能出现的交线数目的集合是（ ）
| A、{0，1，2，3，4，5，6} |
| B、{0，1，3，4，5，6} |
| C、{0，1，2，3，5，6} |
| D、{0，1，3，4} |
一个工人在上班时间[0，5]（单位：小时）内看管两台机器．每天机器出故障的时刻是任意的，一台机器出了故障，就需要一段时间检修，在检修期间另一台机器也出了故障，称为二机器“会面“．如果每台机器的检修时间都是1小时，则此工人在上班时间内，二机器会面的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）存在反函数f-1（x），且f（x）+f（-x）=2，则f-1（x-2）+f-1（4-x）等于（ ）
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
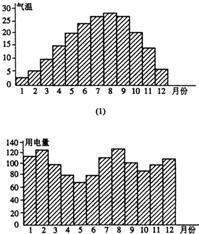一般地，家庭用电量y（千瓦）与气温x（℃）有函数关系y=f（x）．图（1）表示某年12月中每月的平均气温，图（2）表示某家庭在12个月中每月的用电量．试在数集A={x|5≤x≤30，x是2.5的整数倍}中确定一个最小值x1和最大值x2，使y=f（x）是[x1，x2]上的增函数，则区间[x1，x2]=
的二项展开式中，
的系数为