题目内容
解关于x的方程3x2-2（a+2b）x+b2-a2=0．
考点：二次函数的性质
专题：计算题,分类讨论
分析：根据公式求出△，可知方程△≥0再分类讨论，当△=0时，方程有两个相等的根，当△＞0时，方程有两个不相等的根，利用求根公式求解方程的根．
解答：
解：分类讨论，
当△=0时，即△=4（a+2b）2-12（b2-a2）=0，2a=-b时，
此时方程为（x-a）2=0，方程有两个相等的根为x1=x2=a．（5分）
当△＞0时，即△=（2a+b）2＞0，利用求根公式得方程的根为x1=
=
=1，x2=
=
=-1-
．（10分）
当△=0时，即△=4（a+2b）2-12（b2-a2）=0，2a=-b时，
此时方程为（x-a）2=0，方程有两个相等的根为x1=x2=a．（5分）
当△＞0时，即△=（2a+b）2＞0，利用求根公式得方程的根为x1=
-b+
| ||
| 2a |
| -b+2a+b |
| 2a |
-b-
| ||
| 2a |
| -b-2a-b |
| 2a |
| b |
| a |
点评：此题主要考查二次函数的求根公式和关于△的讨论．
练习册系列答案
相关题目
设f（x）是定义域为R的奇函数，且在（0，+∞）上是减函数，若f（1）=0，则不等式f（x）＞0的解集是（ ）
| A、（-∞，-1）∪（1，+∞） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（0，1） |
| D、（-1，0）∪（1，+∞） |
甲、乙、丙三个同学排成一排拍照，则甲排在中间的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）存在反函数f-1（x），且f（x）+f（-x）=2，则f-1（x-2）+f-1（4-x）等于（ ）
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
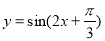在区间
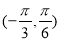内单调递增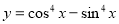
的最小正周期为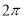
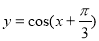的图像是关于点
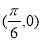成中心对称的图形
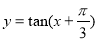的图像是关于直线
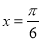成轴对称的图形