题目内容
已知关于x的方程x2-2mx+m+6=0的两个根为x1,x2,求函数y=(x1-1)2+(x2-1)2的最小值.
考点:函数与方程的综合运用
专题:计算题
分析:先根据根与系数的关系利用参数m表示出函数的解析式,必须注意参数m的取值范围,再结合二次函数的图象与性质求出最小值即可.
解答:
解:∵方程x2-2mx+m+6=0的两个根为x1,x2,
∴
且△=4(m2-m-6)≥0,
∴y=(x1-1)2+(x2-1)2=(x1+x2)2-2x1x2-2(x1+x2)+2=4m2-6m-10,
且m≥3或m≤-2.
由二次函数的性质知,当m=3时,
函数y=4m2-6m-10的取得最小值,最小值为:8.
即函数y=(x1-1)2+(x2-1)2的最小值是8.
∴
|
∴y=(x1-1)2+(x2-1)2=(x1+x2)2-2x1x2-2(x1+x2)+2=4m2-6m-10,
且m≥3或m≤-2.
由二次函数的性质知,当m=3时,
函数y=4m2-6m-10的取得最小值,最小值为:8.
即函数y=(x1-1)2+(x2-1)2的最小值是8.
点评:本题主要考查了二次方程根与系数的关系、二次函数最值等函数与方程的综合运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
一个工人在上班时间[0,5](单位:小时)内看管两台机器.每天机器出故障的时刻是任意的,一台机器出了故障,就需要一段时间检修,在检修期间另一台机器也出了故障,称为二机器“会面“.如果每台机器的检修时间都是1小时,则此工人在上班时间内,二机器会面的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)存在反函数f-1(x),且f(x)+f(-x)=2,则f-1(x-2)+f-1(4-x)等于( )
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
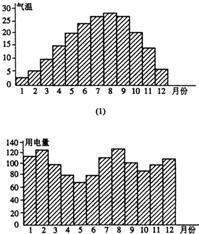 一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]=
一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]=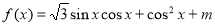 ,
,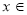
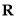 .
. 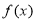 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 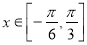 时,
时,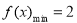 ,求函数
,求函数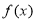 的最大值,并指出
的最大值,并指出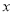 取何值时,函数
取何值时,函数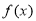 取得最大值.
取得最大值.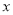 名
名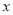 的值
的值