题目内容
已知数列{an}是首项a1>0,q>-1且q≠0的等比数列,设数列{bn}的通项bn=an+1-kan+2(n∈N),数列{an}、{bn}的前n项和分别为Sn,Tn.如果Tn>kSn对一切自然数n都成立,求实数k的取值范围.
考点:数列与不等式的综合,数列的求和,等比数列的性质
专题:计算题
分析:由探寻Tn和Sn的关系入手谋求解题思路.首先利用数列}{bn}与数列{an}的关系确定出数列}{bn}的通项公式和前n项和,即用数列{an}的前n项和表示出数列}{bn}的前n项和,通过不等式有关方法确定出实数k的取值范围.
解答:
解:因为{an}是首项a1>0,公比q>-1且q≠0的等比数列,故
an+1=an•q,an+2=an•q2.
所以bn=an+1-kan+2=an(q-k•q2).
Tn=b1+b2+…+bn=(a1+a2+…+an)(q-k•q2)=Sn(q-kq2).
依题意,由Tn>kSn,得Sn(q-kq2)>kSn,①对一切自然数n都成立.
当q>0时,由a1>0,知an>0,所以Sn>0;
当-1<q<0时,因为a1>0,1-q>0,1-qn>0,所以Sn=
>0
综合上面两种情况,当q>-1且q≠0时,Sn>0总成立.
由①式可得q-kq2>k②,即k<
,
因为-1<q<0,所以-
≤
<0,所以k<-
;
故实数k的取值范围k<-
.
an+1=an•q,an+2=an•q2.
所以bn=an+1-kan+2=an(q-k•q2).
Tn=b1+b2+…+bn=(a1+a2+…+an)(q-k•q2)=Sn(q-kq2).
依题意,由Tn>kSn,得Sn(q-kq2)>kSn,①对一切自然数n都成立.
当q>0时,由a1>0,知an>0,所以Sn>0;
当-1<q<0时,因为a1>0,1-q>0,1-qn>0,所以Sn=
| a1(1-qn) |
| 1-q |
综合上面两种情况,当q>-1且q≠0时,Sn>0总成立.
由①式可得q-kq2>k②,即k<
| q |
| 1+q2 |
因为-1<q<0,所以-
| 1 |
| 2 |
| q |
| 1+q2 |
| 1 |
| 2 |
故实数k的取值范围k<-
| 1 |
| 2 |
点评:本题属于数列与不等式的综合问题,考查学生分析问题解决问题的能力和意识.解决本题的关键要建立两个数列前n项和的联系,通过不等式的分析确定出Sn的正负,简化不等式,得出关于实数k的不等式,考查分离变量思想确定字母取值范围的方法.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
空间四个不同的平面,它们有多种位置关系,从交线数目看,所有可能出现的交线数目的集合是( )
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个工人在上班时间[0,5](单位:小时)内看管两台机器.每天机器出故障的时刻是任意的,一台机器出了故障,就需要一段时间检修,在检修期间另一台机器也出了故障,称为二机器“会面“.如果每台机器的检修时间都是1小时,则此工人在上班时间内,二机器会面的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)存在反函数f-1(x),且f(x)+f(-x)=2,则f-1(x-2)+f-1(4-x)等于( )
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
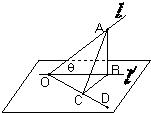 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小. 与函数
与函数
 的图象恰有三个公共点,则实数
的图象恰有三个公共点,则实数 的取值范围是( )
的取值范围是( )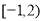 (B)
(B) (C)
(C)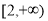 (D)
(D)