题目内容
a+b+c=1,a,b,c∈R+,则abc与
的大小关系是 .
| 1 |
| 27 |
考点:不等式比较大小
专题:证明题
分析:由不等式a+b+c≥3
和a+b+c=1求出二者的关系,注意等号成立的条件.
| 3 | abc |
解答:
解:∵a,b,c∈R+,∴a+b+c≥3
∵a+b+c=1,∴abc≤
(当a=b=c时取等号);
故选Abc≤
| 3 | abc |
∵a+b+c=1,∴abc≤
| 1 |
| 27 |
故选Abc≤
| 1 |
| 27 |
点评:本题利用三个数的基本不等式来判断二者的大小关系,运用了“和为常数,积有最大值”,注意条件:一正二定三相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)存在反函数f-1(x),且f(x)+f(-x)=2,则f-1(x-2)+f-1(4-x)等于( )
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
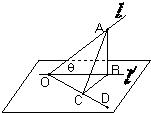 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.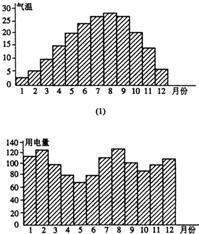 一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]=
一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]= 与函数
与函数
 的图象恰有三个公共点,则实数
的图象恰有三个公共点,则实数 的取值范围是( )
的取值范围是( )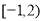 (B)
(B) (C)
(C)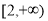 (D)
(D)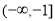
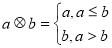 ,令
,令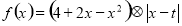 (
(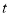 为常数),且
为常数),且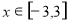 ,则使函数
,则使函数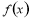 最大值为4的
最大值为4的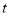 值是( )
值是( ) 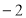 或
或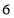 B.
B.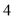 或
或 C.
C.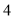 D.
D.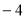 或
或