题目内容
15.已知$1+\frac{1}{1+2}=\frac{4}{3}$,$1+\frac{1}{1+2}+\frac{1}{1+2+3}=\frac{3}{2}$,$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}=\frac{8}{5}$,…,若$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}+…+\frac{1}{1+2+3+…+n}=\frac{12}{7}$,则n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 方法一:直接观察,归纳可得结论,
方法二,求出数列的前n项和,即可求出n.
解答 解:方法一:$1+\frac{1}{1+2}=\frac{4}{3}$=$\frac{2×2}{2+1}$,
$1+\frac{1}{1+2}+\frac{1}{1+2+3}=\frac{3}{2}$=$\frac{6}{4}$=$\frac{2×3}{3+1}$,
$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}=\frac{8}{5}$=$\frac{2×4}{4+1}$
…,
若$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}+…+\frac{1}{1+2+3+…+n}=\frac{12}{7}$=$\frac{2×6}{6+1}$,
∴n=6,
方法二:$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+n}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{2}{n+1}$)=$\frac{2n}{n+1}$,
令$\frac{2n}{n+1}$=$\frac{12}{7}$,
解得n=6
故选:B
点评 本题考查了归纳推理的问题,关键是找到规律,属于中档题.

练习册系列答案
相关题目
5.为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有10人.在20名女性驾驶员中,平均车速超过100km/h的有5人,不超过100km/h的有15人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关;
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过100km/h的车辆数为ζ,若每次抽取的结果是相互独立的,求ζ的分布列和数学期望.
参考公式:${k^2}=\frac{{n(ad-bc{)^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关;
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
参考公式:${k^2}=\frac{{n(ad-bc{)^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在(3,6)内的概率为( )
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
4. 下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
 下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
9.已知是某几何体的三视图,则该几何体的体积为( )
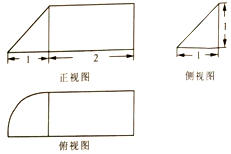

| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
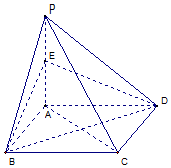 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.