题目内容
16.已知抛物线E:y2=4x,设A、B是抛物线E上分别位于x轴两侧的两个动点,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{9}{4}$(其中O为坐标原点)(Ⅰ)求证:直线AB必过定点,并求出该定点Q的坐标;
(Ⅱ)过点Q作AB的垂线与抛物线交于G、D两点,求四边形AGBD面积的最小值.
分析 (Ⅰ)设出直线AB的方程,联立直线与抛物线方程,利用数量积为0,求出k,化简直线方程推出直线必过定点,并求出该定点Q的坐标;
(Ⅱ)利用韦达定理以及弦长公式,表示出三角形的面积,通过换元法,利用函数的单调性求解最小值即可.
解答 解:(Ⅰ)设直线AB的方程为:x=my+t,A($\frac{{{y}_{1}}^{2}}{4}$,y1)、B($\frac{{{y}_{2}}^{2}}{4}$,y2),
联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+t}\end{array}\right.$得y2-4my-4t=0,则y1+y2=4m,与y1y2=-4t,
由$\overrightarrow{OA}•\overrightarrow{OB}=\frac{9}{4}$得:$\frac{({y}_{1}{y}_{2})^{2}}{16}+{y}_{1}{y}_{2}=\frac{9}{4}$⇒y1y2=-18或y1y2=2(舍).
即$-4t=-18⇒t=\frac{9}{2}$,所以直线AB过定点$Q({\frac{9}{2},0})$;
(Ⅱ)由(Ⅰ)得$|{AB}|=\sqrt{1+{m^2}}|{{y_2}-{y_1}}|$=$\sqrt{1+{m^2}}\sqrt{16{m^2}+72}$,
同理得,$|{GD}|=\sqrt{1+{{({-\frac{1}{m}})}^2}}|{{y_2}-{y_1}}|$=$\sqrt{1+\frac{1}{m^2}}\sqrt{\frac{16}{m^2}+72}$,
则四边形AGBD面积 $S=\frac{1}{2}|{AB}|•|{GD}|=\frac{1}{2}\sqrt{1+{m^2}}$$\sqrt{16{m^2}+72}\sqrt{1+\frac{1}{m^2}}\sqrt{\frac{16}{m^2}+72}$
=$4\sqrt{({2+({{m^2}+\frac{1}{m^2}})})•({85+18({{m^2}+\frac{1}{m^2}})})}$,
令${m^2}+\frac{1}{m^2}=μ({μ≥2})$,
则$S=4\sqrt{18{μ^2}+121μ+170}$是对称轴为μ<0,开口向上,函数是关于μ的增函数,当μ=2时函数取得最小值.
故Smin=88.
当且仅当m=1时取到最小值88.
点评 本题考查直线与抛物线的位置关系的综合应用,韦达定理以及弦长公式,函数与方程思想的应用,考查转化思想以及计算能力.

 下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
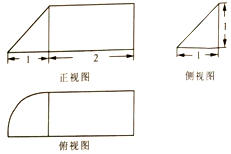
| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
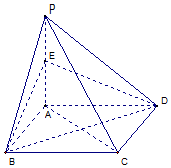 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.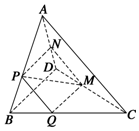 如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).
如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).